Appendix C — Probability

---

Configuring R

Functions from these packages will be used throughout this document:

library(conflicted) # check for conflicting function definitions
# library(printr) # inserts help-file output into markdown output
library(rmarkdown) # Convert R Markdown documents into a variety of formats.
library(pander) # format tables for markdown
library(ggplot2) # graphics
library(ggeasy) # help with graphics
library(ggfortify) # help with graphics
library(dplyr) # manipulate data
library(tibble) # `tibble`s extend `data.frame`s
library(magrittr) # `%>%` and other additional piping tools
library(haven) # import Stata files
library(knitr) # format R output for markdown
library(tidyr) # Tools to help to create tidy data
library(plotly) # interactive graphics
library(dobson) # datasets from Dobson and Barnett 2018
library(parameters) # format model output tables for markdown
library(haven) # import Stata files
library(latex2exp) # use LaTeX in R code (for figures and tables)
library(fs) # filesystem path manipulations
library(survival) # survival analysis
library(survminer) # survival analysis graphics
library(KMsurv) # datasets from Klein and Moeschberger
library(parameters) # format model output tables for
library(webshot2) # convert interactive content to static for pdf
library(forcats) # functions for categorical variables ("factors")
library(stringr) # functions for dealing with strings
library(lubridate) # functions for dealing with dates and times

Here are some R settings I use in this document:

rm(list = ls()) # delete any data that's already loaded into R

conflicts_prefer(dplyr::filter)
ggplot2::theme_set(
  ggplot2::theme_bw() + 
        # ggplot2::labs(col = "") +
    ggplot2::theme(
      legend.position = "bottom",
      text = ggplot2::element_text(size = 12, family = "serif")))

knitr::opts_chunk$set(message = FALSE)
options('digits' = 6)

panderOptions("big.mark", ",")
pander::panderOptions("table.emphasize.rownames", FALSE)
pander::panderOptions("table.split.table", Inf)
conflicts_prefer(dplyr::filter) # use the `filter()` function from dplyr() by default
legend_text_size = 9
run_graphs = TRUE

---

Most of the content in this chapter should be review from UC Davis Epi 202.

C.1 Core properties of probabilities

C.1.1 Defining probabilities

Definition C.1 (Probability measure) A probability measure, often denoted \(\Pr()\) or \(\text{P}()\), is a function whose domain is a \(\sigma\)-algebra of possible outcomes, \(\mathscr{S}\), and which satisfies the following properties:

1. For any statistical event \(A \in \mathscr{S}\), \(\Pr(A) \ge 0\).

2. The probability of the union of all outcomes (\(\Omega \stackrel{\text{def}}{=}\cup \mathscr{S}\)) is 1:

\[\Pr(\Omega) = 1\]

3. The probability of the union of disjoint events, \(A_1 \cup A_2: A_1 \cap A_2 = \emptyset\), is equal to the sum of their probabilities:

\[\Pr(A_1 \cup A_2) = \Pr(A_1) + \Pr(A_2)\]

---

Theorem C.1 If \(A\) and \(B\) are statistical events and \(A\subseteq B\), then \(\Pr(A \cap B) = \Pr(A)\).

---

Proof. Left to the reader for now.

---

Theorem C.2 \[\Pr(A) + \Pr(\neg A) = 1\]

---

Proof. By properties 2 and 3 of Definition C.1.

---

Corollary C.1 \[\Pr(\neg A) = 1 - \Pr(A)\]

---

Proof. By Theorem C.2 and algebra.

---

Corollary C.2 If the probability of an outcome \(A\) is \(\Pr(A)=\pi\), then the probability that \(A\) does not occur is:

\[\Pr(\neg A)= 1 - \pi\]

---

Proof. Using Corollary C.1:

\[ \begin{aligned} \Pr(\neg A) &= 1 - \Pr(A) \\ &= 1 - \pi \end{aligned} \]

C.2 Random variables

C.2.1 Binary variables

Definition C.2 (binary variable) A binary variable is a random variable which has only two possible values in its range.

Exercise C.1 (Examples of binary variables) What are some examples of binary variables in the health sciences?

---

Solution. Examples of binary outcomes include:

• exposure (exposed vs unexposed)
• disease (diseased vs healthy)
• recovery (recovered vs unrecovered)
• relapse (relapse vs remission)
• return to hospital (returned vs not)
• vital status (dead vs alive)

---

C.2.2 Count variables

Definition C.3 (Count variable) A count variable is a random variable whose possible values are some subset of the non-negative integers; that is, a random variable \(X\) such that:

\[\mathcal{R}(X) \in \text{N}\]

---

Exercise C.2 What are some examples of count variables?

---

Solution.

• Number of fish in a pond
• Number of cyclones per season
• Seconds of tooth-brushing per session (if rounded)
• Infections per person-year
• Visits to ER per person-month
• Car accidents per 1000 miles driven

---

Definition C.4 (Exposure magnitude) For many count outcomes, there is some sense of an exposure magnitude, such as population size, or duration of observation, which multiplicatively rescales the expected (mean) count.

---

Exercise C.3 What are some examples of exposure magnitudes?

---

Solution.

Table C.1: Examples of exposure units

outcome	exposure units
disease incidence	number of individuals exposed; time at risk
car accidents	miles driven
worksite accidents	person-hours worked
population size	size of habitat

Exposure units are similar to the number of trials in a binomial distribution, but in non-binomial count outcomes, there can be more than one event per unit of exposure.

We can use \(t\) to represent continuous-valued exposures/observation durations, and \(n\) to represent discrete-valued exposures.

---

Definition C.5 (Event rate)  

For a count outcome \(Y\) with exposure magnitude \(t\), the event rate (denoted \(\lambda\)) is defined as the mean of \(Y\) divided by the exposure magnitude. That is:

\[\mu \stackrel{\text{def}}{=}\text{E}[Y|T=t]\]

\[\lambda \stackrel{\text{def}}{=}\frac{\mu}{t} \tag{C.1}\]

Event rate is somewhat analogous to odds in binary outcome models; it typically serves as an intermediate transformation between the mean of the outcome and the linear component of the model. However, in contrast with the odds function, the transformation \(\lambda = \mu/t\) is not considered part of the Poisson model’s link function, and it treats the exposure magnitude covariate differently from the other covariates.

---

Theorem C.3 (Transformation function from event rate to mean) For a count variable with mean \(\mu\), event rate \(\lambda\), and exposure magnitude \(t\):

\[\therefore\mu = \lambda \cdot t \tag{C.2}\]

---

Solution. Start from definition of event rate and use algebra to solve for \(\mu\).

---

Equation C.2 is analogous to the inverse-odds function for binary variables.

---

Theorem C.4 When the exposure magnitude is 0, there is no opportunity for events to occur:

\[\text{E}[Y|T=0] = 0\]

---

Proof. \[\text{E}[Y|T=0] = \lambda \cdot 0 = 0\]

---

Probability distributions for count outcomes

• Poisson distribution

• Negative binomial distribution

---

C.3 Key probability distributions

---

Some distributions are typically used for outcome models (Table C.2); other distributions are typically used for test statistics (Table C.3).

Table C.2: Distributions typically used for outcome models

Distribution	Uses
Bernoulli	Binary outcomes
Binomial	Sums of Bernoulli outcomes
Poisson	unbounded count outcomes
Geometric	Counts of non-events before an event occurs
Negative binomal	Mixtures of Poisson distributions, counts of non-events until a given number of events occurs
Normal (Gaussian)	Continuous outcomes without a more specific distribution
exponential	Time to event outcomes
Gamma	Time to event outcomes
Weibull	Time to event outcomes
Log-normal	Time to event outcomes

---

Table C.3: Distributions typically used for test statistics

Distribution	Uses
\(\chi^2\)	Regression comparisons (asymptotic), contingency table independence tests, goodness-of-fit tests
\(F\)	Gaussian model comparisons (exact)
\(Z\) (standard normal)	Proportions, means, regression coefficients (asymptotic)
\(T\)	Means, regression coefficients in Gaussian outcome models (exact)

C.3.1 The Bernoulli distribution

Definition C.6 (Bernoulli distribution) The Bernoulli distribution family for a random variable \(X\) is defined as:

\[ \begin{aligned} \Pr(X=x) &= \text{1}_{x\in {\left\{0,1\right\}}}\pi^x(1-\pi)^{1-x}\\ &= \left\{{\pi, x=1}\atop{1-\pi, x=0}\right. \end{aligned} \]

---

C.3.2 The Poisson distribution

Figure C.1: “Les Poissons”

Siméon Denis Poisson

Les Poissons

---

Definition C.7 (Poisson distribution) \[\mathcal{R}(Y) = {\left\{0, 1, 2, ...\right\}} = \text{N}\]

\[\text{P}(Y = y) = \frac{\mu^{y} e^{-\mu}}{y!}, y \in \text{N} \tag{C.3}\]

(see Figure C.2)

\[\text{P}(Y \le y) = e^{-\mu} \sum_{j=0}^{\left \lfloor{y}\right \rfloor}\frac{\mu^j}{j!} \tag{C.4}\]

(see Figure C.3)

---

library(dplyr)
pois_dists = tibble(
  mu = c(0.5, 1, 2, 5, 10, 20)) |> 
  reframe(
    .by = mu,
    x = 0:30
  ) |> 
  mutate(
    `P(X = x)` = dpois(x, lambda = mu),
    `P(X <= x)` = ppois(x, lambda = mu),
    mu = factor(mu)
  )

library(ggplot2)
library(latex2exp)

plot0 = pois_dists |> 
  ggplot(
    aes(
      x = x,
      y = `P(X = x)`,
      fill = mu,
      col = mu)) +
  theme(legend.position = "bottom") +
  labs(
    fill = latex2exp::TeX("$\\mu$"),
    col = latex2exp::TeX("$\\mu$"),
    y = latex2exp::TeX("$\\Pr_{\\mu}(X = x)$"))

plot1 = plot0 + 
  geom_col(position = "identity", alpha  = .5) +
  facet_wrap(~mu)
  # geom_point(alpha = 0.75) +
  # geom_line(alpha = 0.75)
print(plot1)

Figure C.2: Poisson PMFs, by mean parameter \(\mu\)

---

library(ggplot2)

plot2 = 
  plot0 + 
  geom_step(alpha = 0.75) +
  aes(y = `P(X <= x)`) + 
  labs(y = latex2exp::TeX("$\\Pr_{\\mu}(X \\leq x)$"))

print(plot2)

Figure C.3: Poisson CDFs

---

Exercise C.4 (Poisson distribution functions) Let \(X \sim \text{Pois}(\mu = 3.75)\).

Compute:

• \(\text{P}(X = 4 | \mu = 3.75)\)
• \(\text{P}(X \le 7 | \mu = 3.75)\)
• \(\text{P}(X > 5 | \mu = 3.75)\)

---

Solution.

• \(\text{P}(X=4) = 0.19378\)
• \(\text{P}(X\le 7) = 0.962379\)
• \(\text{P}(X > 5) = 0.177117\)

---

Theorem C.5 (Properties of the Poisson distribution) If \(X \sim \text{Pois}(\mu)\), then:

• \(\text{E}[X] = \mu\)
• \(\text{Var}(X) = \mu\)
• \(\text{P}(X=x) = \frac{\mu}{x} \text{P}(X = x-1)\)
• For \(x < \mu\), \(\text{P}(X=x) > \text{P}(X = x-1)\)
• For \(x = \mu\), \(\text{P}(X=x) = \text{P}(X = x-1)\)
• For \(x > \mu\), \(\text{P}(X=x) < \text{P}(X = x-1)\)
• \(\arg \max_{x} \text{P}(X=x) = \left \lfloor{\mu}\right \rfloor\)

Exercise C.5 Prove Theorem C.5.

---

Solution. \[ \begin{aligned} \text{E}[X] &= \sum_{x=0}^\infty x \cdot P(X=x)\\ &= 0 \cdot P(X=0) + \sum_{x=1}^\infty x \cdot P(X=x)\\ &= 0 + \sum_{x=1}^\infty x \cdot P(X=x)\\ &= \sum_{x=1}^\infty x \cdot P(X=x)\\ &= \sum_{x=1}^\infty x \cdot \frac{\lambda^x e^{-\lambda}}{x!}\\ &= \sum_{x=1}^\infty x \cdot \frac{\lambda^x e^{-\lambda}}{x \cdot (x-1)!} & [\text{definition of factorial ("!") function}]\\ &= \sum_{x=1}^\infty \frac{\lambda^x e^{-\lambda}}{ (x-1)!}\\ &= \sum_{x=1}^\infty \frac{(\lambda \cdot \lambda^{x-1}) e^{-\lambda}}{ (x-1)!}\\ &= \lambda \cdot \sum_{x=1}^\infty \frac{( \lambda^{x-1}) e^{-\lambda}}{ (x-1)!}\\ &= \lambda \cdot \sum_{y=0}^\infty \frac{( \lambda^{y}) e^{-\lambda}}{ (y)!} &[\text{substituting } y \stackrel{\text{def}}{=}x-1]\\ &= \lambda \cdot 1 &[\text{because PDFs sum to 1}]\\ &= \lambda\\ \end{aligned} \]

See also https://statproofbook.github.io/P/poiss-mean.

For the variance, see https://statproofbook.github.io/P/poiss-var.

---

Accounting for exposure

If the exposures/observation durations, denoted \(T=t\) or \(N=n\), vary between observations, we model:

\[\mu = \lambda\cdot t\]

\(\lambda\) is interpreted as the “expected event rate per unit of exposure”; that is,

\[\lambda = \frac{\text{E}[Y|T=t]}{t}\]

Important

The exposure magnitude, \(T\), is similar to a covariate in linear or logistic regression. However, there is an important difference: in count regression, there is no intercept corresponding to \(\text{E}[Y|T=0]\). In other words, this model assumes that if there is no exposure, there can’t be any events.

Theorem C.6 If \(\mu = \lambda\cdot t\), then:

\[\log{\mu} = \log{\lambda} + \log{t}\]

Definition C.8 (Offset) When the linear component of a model involves a term without an unknown coefficient, that term is called an offset.

---

Theorem C.7 If \(X\) and \(Y\) are independent Poisson random variables with means \(\mu_X\) and \(\mu_Y\), their sum, \(Z=X+Y\), is also a Poisson random variable, with mean \(\mu_Z = \mu_X + \mu_Y\).

---

Proof. See https://web.stanford.edu/class/archive/cs/cs109/cs109.1206/lectureNotes/LN12_independent_rvs.pdf, Example 3.

---

C.3.3 The Negative-Binomial distribution

Definition C.9 (Negative binomial distribution) \[ \text{P}(Y=y) = \frac{\mu^y}{y!} \cdot \frac{\Gamma(\rho + y)}{\Gamma(\rho) \cdot (\rho + \mu)^y} \cdot \left(1+\frac{\mu}{\rho}\right)^{-\rho} \]

where \(\rho\) is an overdispersion parameter and \(\Gamma(x) = (x-1)!\) for integers \(x\).

You don’t need to memorize or understand this expression.

As \(\rho \rightarrow \infty\), the second term converges to 1 and the third term converges to \(\text{exp}{\left\{-\mu\right\}}\), which brings us back to the Poisson distribution.

---

Theorem C.8 If \(Y \sim \text{NegBin}(\mu, \rho)\), then:

• \(\text{E}[Y] = \mu\)
• \(\text{Var}{\left(Y\right)} = \mu + \frac{\mu^2}{\rho} > \mu\)

C.3.4 Weibull Distribution

\[ \begin{aligned} p(t)&= \alpha\lambda x^{\alpha-1}\text{e}^{-\lambda x^\alpha}\\ {\lambda}(t)&=\alpha\lambda x^{\alpha-1}\\ \text{S}(t)&=\text{e}^{-\lambda x^\alpha}\\ E(T)&= \Gamma(1+1/\alpha)\cdot \lambda^{-1/\alpha} \end{aligned} \]

When \(\alpha=1\) this is the exponential. When \(\alpha>1\) the hazard is increasing and when \(\alpha < 1\) the hazard is decreasing. This provides more flexibility than the exponential.

We will see more of this distribution later.

C.4 Characteristics of probability distributions

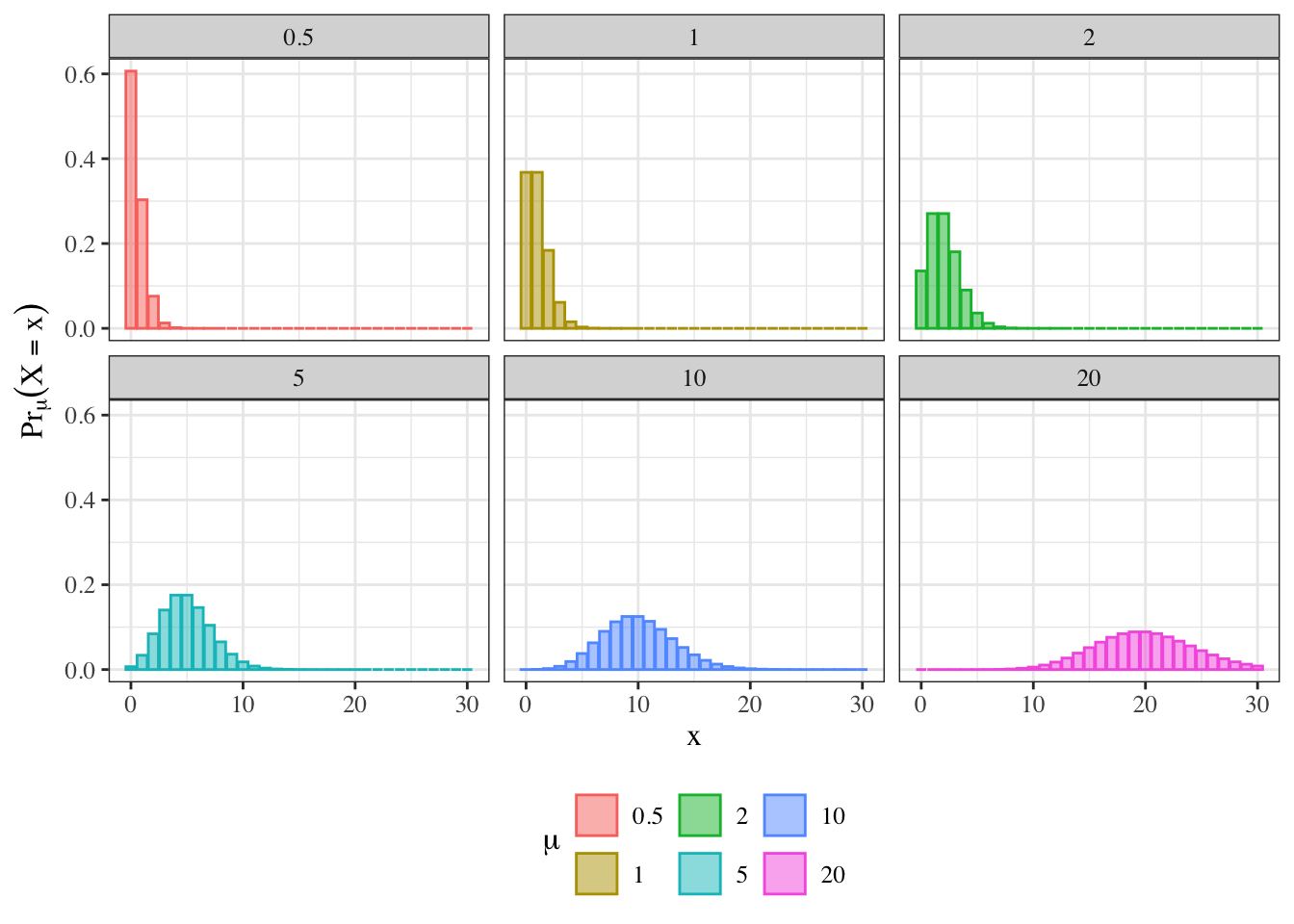
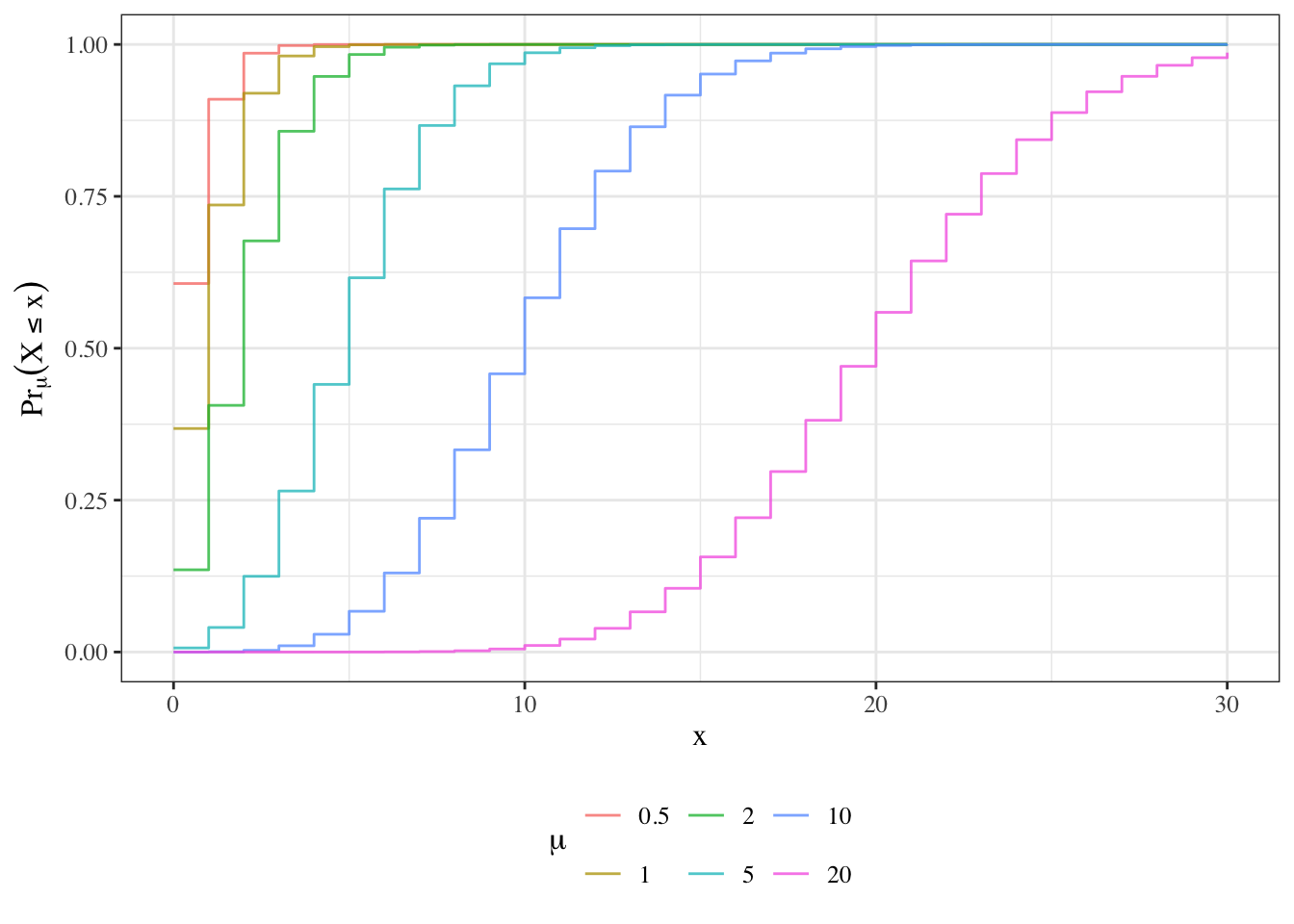
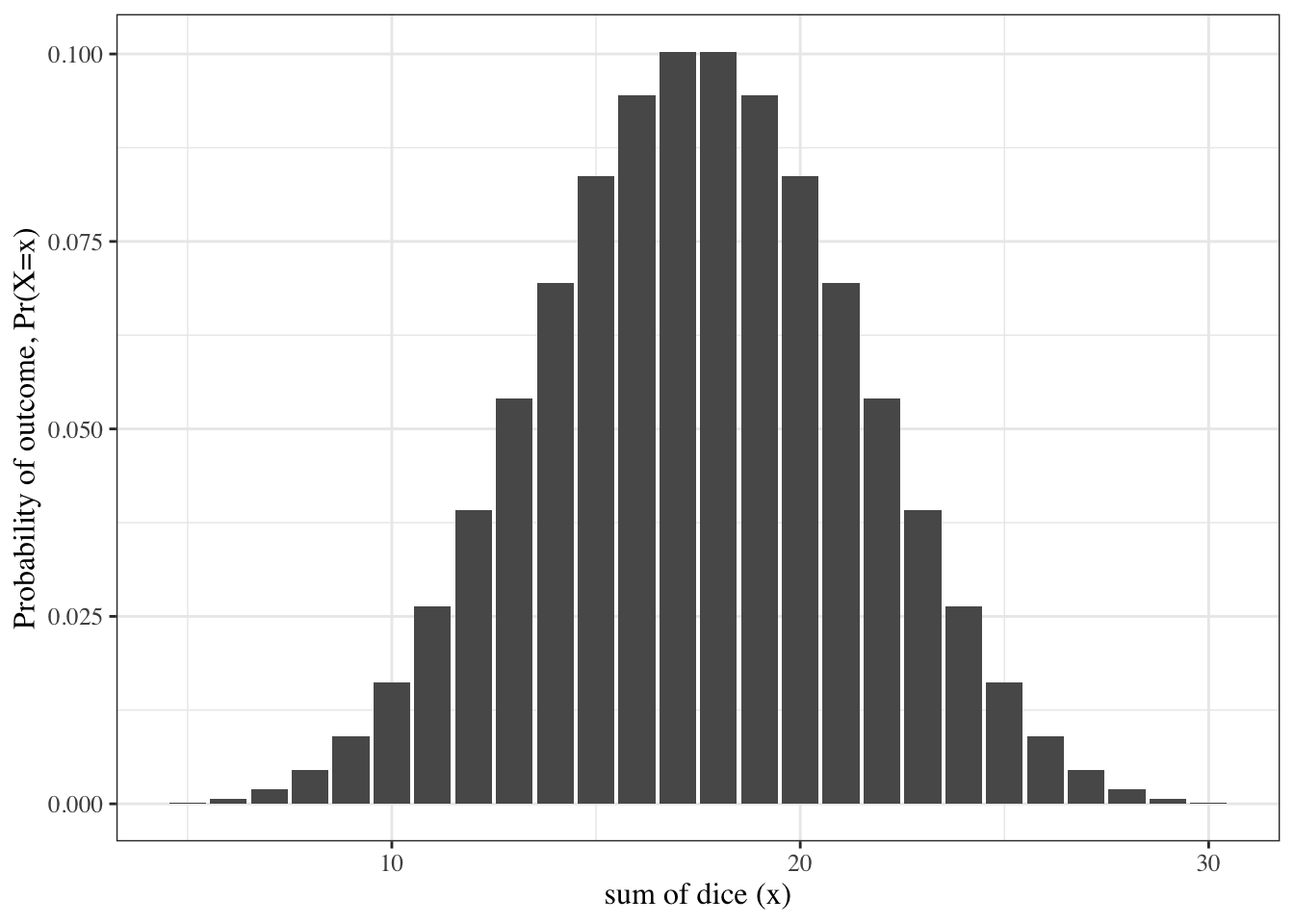
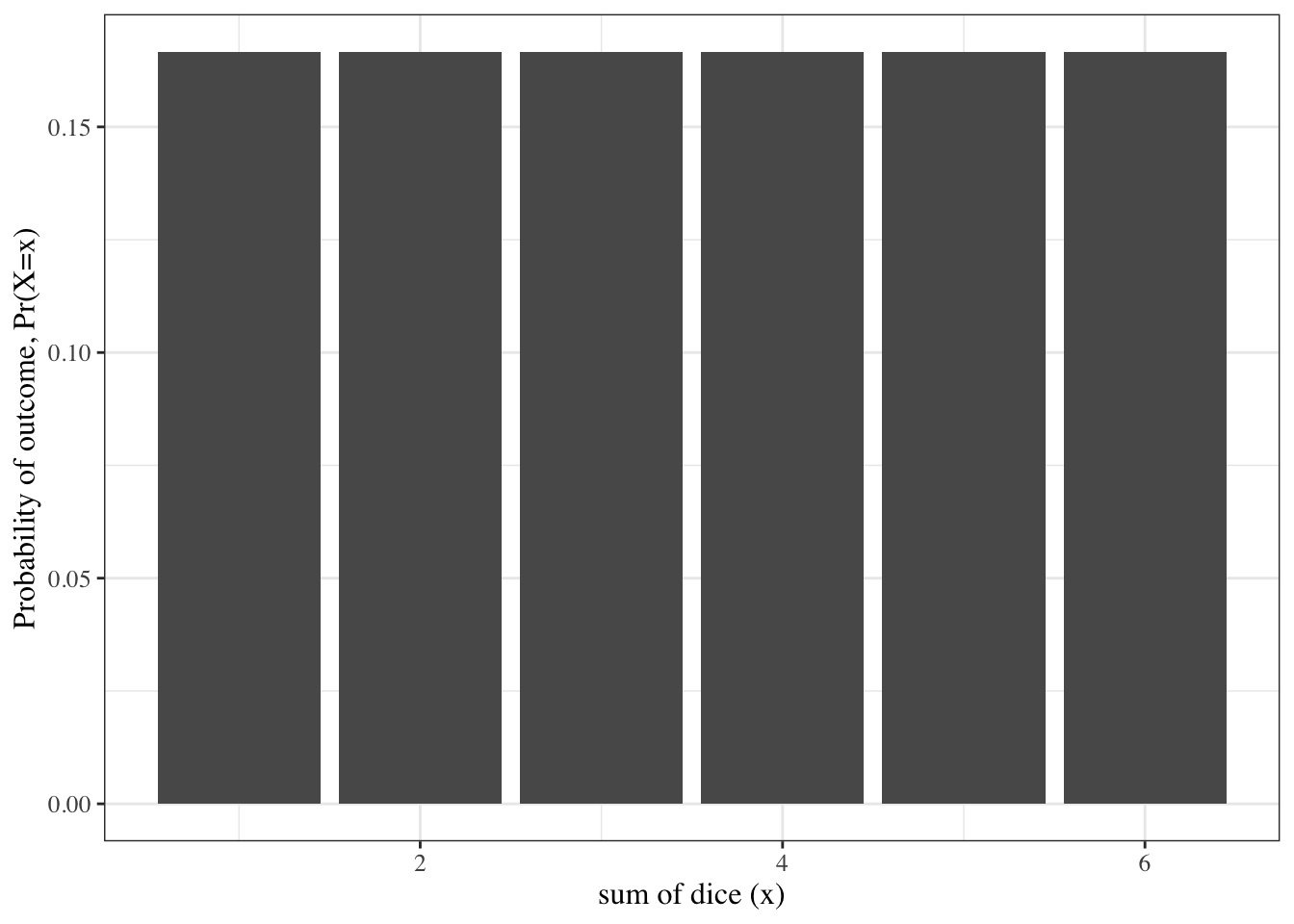
C.4.1 Probability density function

Definition C.10 (probability density) If \(X\) is a continuous random variable, then the probability density of \(X\) at value \(x\), denoted \(f(x)\), \(f_X(x)\), \(\text{p}(x)\), \(\text{p}_X(x)\), or \(\text{p}(X=x)\), is defined as the limit of the probability (mass) that \(X\) is in an interval around \(x\), divided by the width of that interval, as that width reduces to 0.

\[ \begin{aligned} f(x) &\stackrel{\text{def}}{=}\lim_{\Delta \rightarrow 0} \frac{\text{P}(X \in [x, x + \Delta])}{\Delta} \end{aligned} \]

See also Rothman et al. (2021) (Chapter 22, p. 535) and https://en.wikipedia.org/wiki/Probability_density_function#Formal_definition

---

Theorem C.9 (Density function is derivative of CDF) The density function \(f(t)\) or \(\text{p}(T=t)\) for a random variable \(T\) at value \(t\) is equal to the derivative of the cumulative probability function \(F(t) \stackrel{\text{def}}{=}P(T\le t)\); that is:

\[f(t) \stackrel{\text{def}}{=}\frac{\partial}{\partial t} F(t)\]

---

Theorem C.10 (Density functions integrate to 1) For any density function \(f(x)\),

\[\int_{x \in \mathcal{R}(X)} f(x) dx = 1\]

---

C.4.2 Hazard function

Definition C.11 (Hazard function, hazard rate, hazard rate function)  

The hazard function, hazard rate, hazard rate function, for a random variable \(T\) at value \(t\), typically denoted as \(\text{h}(t)\) ¹ or \(\lambda(t)\), ² is the conditional density of \(T\) at \(t\), given \(T \ge t\). That is:

\[{\lambda}(t) \stackrel{\text{def}}{=}\text{p}(T=t|T\ge t)\]

If \(T\) represents the time at which an event occurs, then \({\lambda}(t)\) is the probability that the event occurs at time \(t\), given that it has not occurred prior to time \(t\).

---

Table C.4: Probability distribution functions

Name	Symbols	Definition
Probability density function (PDF)	\(\text{f}(t), \text{p}(t)\)	\(\text{p}(T=t)\)
Cumulative distribution function (CDF)	\(\text{F}(t), \text{P}(t)\)	\(\text{P}(T\leq t)\)
Survival function	\(\text{S}(t), \bar{\text{F}}(t)\)	\(\text{P}(T > t)\)
Hazard function	\(\lambda(t), \text{h}(t)\)	\(\text{p}(T=t|T\ge t)\)
Cumulative hazard function	\(\Lambda(t), \text{H}(t)\)	\(\int_{u=-\infty}^t {\lambda}(u)du\)
Log-hazard function	\(\eta(t)\)	\(\text{log}{\left\{{\lambda}(t)\right\}}\)

---

\[ \text{f}(t) \xleftarrow[\text{S}(t){\lambda}(t)]{-S'(t)} \text{S}(t) \xleftarrow[]{\text{exp}{\left\{-{\Lambda}(t)\right\}}} {\Lambda}(t) \xleftarrow[]{\int_{u=0}^t {\lambda}(u)du} {\lambda}(t) \xleftarrow[]{\text{exp}{\left\{\eta(t)\right\}}} \eta(t) \]

\[ \text{f}(t) \xrightarrow[\int_{u=t}^\infty \text{f}(u)du]{\text{f}(t)/{\lambda}(t)} \text{S}(t) \xrightarrow[-\log{\text{S}(t)}]{} {\Lambda}(t) \xrightarrow[{\Lambda}'(t)]{} {\lambda}(t) \xrightarrow[\text{log}{\left\{{\lambda}(t)\right\}}]{} \eta(t) \]

---

C.4.3 Expectation

Definition C.12 (Expectation, expected value, population mean ) The expectation, expected value, or population mean of a continuous random variable \(X\), denoted \(\text{E}{\left[X\right]}\), \(\mu(X)\), or \(\mu_X\), is the weighted mean of \(X\)’s possible values, weighted by the probability density function of those values:

\[\text{E}{\left[X\right]} = \int_{x\in \mathcal{R}(X)} x \cdot \text{p}(X=x)dx\]

The expectation, expected value, or population mean of a discrete random variable \(X\), denoted \(\text{E}{\left[X\right]}\), \(\mu(X)\), or \(\mu_X\), is the mean of \(X\)’s possible values, weighted by the probability mass function of those values:

\[\text{E}{\left[X\right]} = \sum_{x \in \mathcal{R}(X)} x \cdot \text{P}(X=x)\]

(c.f. https://en.wikipedia.org/wiki/Expected_value)

---

Theorem C.11 (Expectation of the Bernoulli distribution) The expectation of a Bernoulli random variable with parameter \(\pi\) is:

\[\text{E}{\left[X\right]} = \pi\]

---

Proof. \[ \begin{aligned} \text{E}{\left[X\right]} &= \sum_{x\in \mathcal{R}(X)} x \cdot\text{P}(X=x) \\&= \sum_{x\in {\left\{0,1\right\}}} x \cdot\text{P}(X=x) \\&= {\left(0 \cdot\text{P}(X=0)\right)} + {\left(1 \cdot\text{P}(X=1)\right)} \\&= {\left(0 \cdot(1-\pi)\right)} + {\left(1 \cdot\pi\right)} \\&= 0 + \pi \\&= \pi \end{aligned} \]

---

Theorem C.12 (Expectation of time-to-event variables) If \(T\) is a non-negative random variable, then:

\[\mu(T|\tilde{X}= \tilde{x}) = \int_{t=0}^{\infty}\text{S}(t)dt\]

---

C.4.4 Variance and related characteristics

Definition C.13 (Variance) The variance of a random variable \(X\) is the expectation of the squared difference between \(X\) and \(\text{E}{\left[X\right]}\); that is:

\[ \text{Var}{\left(X\right)} \stackrel{\text{def}}{=}\text{E}{\left[(X-\text{E}{\left[X\right]})^2\right]} \]

---

Theorem C.13 (Simplified expression for variance) \[\text{Var}{\left(X\right)}=\text{E}{\left[X^2\right]} - {\left(\text{E}{\left[X\right]}\right)}^2\]

---

Proof. By linearity of expectation, we have:

\[ \begin{aligned} \text{Var}{\left(X\right)} &\stackrel{\text{def}}{=}\text{E}{\left[(X-\text{E}{\left[X\right]})^2\right]}\\ &=\text{E}{\left[X^2 - 2X\text{E}{\left[X\right]} + {\left(\text{E}{\left[X\right]}\right)}^2\right]}\\ &=\text{E}{\left[X^2\right]} - \text{E}{\left[2X\text{E}{\left[X\right]}\right]} + \text{E}{\left[{\left(\text{E}{\left[X\right]}\right)}^2\right]}\\ &=\text{E}{\left[X^2\right]} - 2\text{E}{\left[X\right]}\text{E}{\left[X\right]} + {\left(\text{E}{\left[X\right]}\right)}^2\\ &=\text{E}{\left[X^2\right]} - {\left(\text{E}{\left[X\right]}\right)}^2\\ \end{aligned} \]

---

Definition C.14 (Precision) The precision of a random variable \(X\), often denoted \(\tau(X)\), \(\tau_X\), or shorthanded as \(\tau\), is the inverse of that random variable’s variance; that is:

\[\tau(X) \stackrel{\text{def}}{=}{\left(\text{Var}{\left(X\right)}\right)}^{-1}\]

Definition C.15 (Standard deviation) The standard deviation of a random variable \(X\) is the square-root of the variance of \(X\):

\[\text{SD}{\left(X\right)} \stackrel{\text{def}}{=}\sqrt{\text{Var}{\left(X\right)}}\]

---

Definition C.16 (Covariance) For any two one-dimensional random variables, \(X,Y\):

\[\text{Cov}{\left(X,Y\right)} \stackrel{\text{def}}{=}\text{E}{\left[(X - \text{E}{\left[X\right]})(Y - \text{E}{\left[Y\right]})\right]}\]

---

Theorem C.14 \[\text{Cov}{\left(X,Y\right)}= \text{E}{\left[XY\right]} - \text{E}{\left[X\right]} \text{E}{\left[Y\right]}\]

---

Proof. Left to the reader.

---

Lemma C.1 (The covariance of a variable with itself is its variance) For any random variable \(X\):

\[\text{Cov}{\left(X,X\right)} = \text{Var}{\left(X\right)}\]

Proof. \[ \begin{aligned} \text{Cov}{\left(X,X\right)} &= E[XX] - E[X]E[X] \\ &= E[X^2]-(E[X])^2 \\ &= \text{Var}{\left(X\right)} \end{aligned} \]

---

Definition C.17 (Variance/covariance of a \(p \times 1\) random vector) For a \(p \times 1\) dimensional random vector \(\tilde{X}\),

\[ \begin{aligned} \text{Var}{\left(\tilde{X}\right)} &\stackrel{\text{def}}{=}\text{Cov}{\left(\tilde{X}\right)} \\ &\stackrel{\text{def}}{=}\text{E}{\left[{\left(\tilde{X}- \text{E}\tilde{X}\right)}^{\top} {\left(\tilde{X}- \text{E}\tilde{X}\right)}\right]} \end{aligned} \]

---

Theorem C.15 (Alternate expression for variance of a random vector) \[ \begin{aligned} \text{Var}{\left(X\right)} &= E[ X^{\top}X ] - {E\lbrack X\rbrack}^{\top}E\lbrack X\rbrack \end{aligned} \]

---

Proof. \[ \begin{aligned} \text{Var}{\left(X\right)} &= E[ \left( X^{\top} - E\lbrack X\rbrack^{\top} \right)\left( X - E\lbrack X\rbrack \right) ]\\ &= E[ X^{\top}X - E\lbrack X\rbrack^{\top}X - X^{\top}E\lbrack X\rbrack + E\lbrack X\rbrack^{\top}E\lbrack X\rbrack ]\\ &= E[ X^{\top}X ] - E\lbrack X\rbrack^{\top}E\lbrack X\rbrack - {E\lbrack X\rbrack}^{\top}E\lbrack X\rbrack + E\lbrack X\rbrack^{\top}E\lbrack X\rbrack\\ &= E[ X^{\top}X ] - 2{E\lbrack X\rbrack}^{\top}E\lbrack X\rbrack + E\lbrack X\rbrack^{\top}E\lbrack X\rbrack\\ &= E[ X^{\top}X ] - {E\lbrack X\rbrack}^{\top}E\lbrack X\rbrack \end{aligned} \]

---

Theorem C.16 (Variance of a linear combination) For any vector of random variables \(\tilde{X}= (X_1, \ldots, X_n)\) and corresponding vector of constants \(\tilde{a}= (a_1, ... ,a_n)\), the variance of their linear combination is:

\[ \begin{aligned} \text{Var}{\left(\tilde{a}\cdot \tilde{X}\right)} &= \text{Var}{\left(\sum_{i=1}^na_i X_i\right)} \\ &= \tilde{a}^{\top} \text{Var}{\left(\tilde{X}\right)} \tilde{a} \\ &= \sum_{i=1}^n\sum_{j=1}^n a_i a_j \text{Cov}{\left(X_i,X_j\right)} \end{aligned} \]

---

Proof. Left to the reader…

---

Corollary C.3 For any two random variables \(X\) and \(Y\) and scalars \(a\) and \(b\):

\[\text{Var}{\left(aX + bY\right)} = a^2 \text{Var}{\left(X\right)} + b^2 \text{Var}{\left(Y\right)} + 2(a \cdot b) \text{Cov}{\left(X,Y\right)}\]

---

Proof. Apply Theorem C.16 with \(n=2\), \(X_1 = X\), and \(X_2 = Y\).

Or, see https://statproofbook.github.io/P/var-lincomb.html

---

Definition C.18 (homoskedastic, heteroskedastic) A random variable \(Y\) is homoskedastic (with respect to covariates \(X\)) if the variance of \(Y\) does not vary with \(X\):

\[\text{Var}(Y|X=x) = \sigma^2, \forall x\]

Otherwise it is heteroskedastic.

---

Definition C.19 (Statistical independence) A set of random variables \(X_1, \ldots, X_n\) are statistically independent if their joint probability is equal to the product of their marginal probabilities:

\[\Pr(X_1=x_1, \ldots, X_n = x_n) = \prod_{i=1}^n{\Pr(X_i=x_i)}\]

Tip

The symbol for independence, \(\perp\!\!\!\perp\), is essentially just \(\prod\) upside-down. So the symbol can remind you of its definition (Definition C.19).

---

Definition C.20 (Conditional independence) A set of random variables \(Y_1, \ldots, Y_n\) are conditionally statistically independent given a set of covariates \(X_1, \ldots, X_n\) if the joint probability of the \(Y_i\)s given the \(X_i\)s is equal to the product of their marginal probabilities:

\[\Pr(Y_1=y_1, \ldots, Y_n = y_n|X_1=x_1, \ldots, X_n = x_n) = \prod_{i=1}^n{\Pr(Y_i=y_i|X_i=x_i)}\]

---

Definition C.21 (Identically distributed) A set of random variables \(X_1, \ldots, X_n\) are identically distributed if they have the same range \(\mathcal{R}(X)\) and if their marginal distributions \(\text{P}(X_1=x_1), ..., \text{P}(X_n=x_n)\) are all equal to some shared distribution \(\text{P}(X=x)\):

\[ \forall i\in {\left\{1:n\right\}}, \forall x \in \mathcal{R}(X): \text{P}(X_i=x) = \text{P}(X=x) \]

---

Definition C.22 (Conditionally identically distributed) A set of random variables \(Y_1, \ldots, Y_n\) are conditionally identically distributed given a set of covariates \(X_1, \ldots, X_n\) if \(Y_1, \ldots, Y_n\) have the same range \(\mathcal{R}(X)\) and if the distributions \(\text{P}(Y_i=y_i|X_i =x_i)\) are all equal to the same distribution \(\text{P}(Y=y|X=x)\):

\[ \text{P}(Y_i=y|X_i=x) = \text{P}(Y=y|X=x) \]

---

Definition C.23 (Independent and identically distributed) A set of random variables \(X_1, \ldots, X_n\) are independent and identically distributed (shorthand: “\(X_i\ \text{iid}\)”) if they are statistically independent and identically distributed.

---

Definition C.24 (Conditionally independent and identically distributed) A set of random variables \(Y_1, \ldots, Y_n\) are conditionally independent and identically distributed (shorthand: “\(Y_i | X_i\ \text{ciid}\)” or just “\(Y_i |X_i\ \text{iid}\)”) given a set of covariates \(X_1, \ldots, X_n\) if \(Y_1, \ldots, Y_n\) are conditionally independent given \(X_1, \ldots, X_n\) and \(Y_1, \ldots, Y_n\) are identically distributed given \(X_1, \ldots, X_n\).

C.5 The Central Limit Theorem

The sum of many independent or nearly-independent random variables with small variances (relative to the number of RVs being summed) produces bell-shaped distributions.

For example, consider the sum of five dice (Figure C.4).

library(dplyr)
dist = 
  expand.grid(1:6, 1:6, 1:6, 1:6, 1:6) |> 
  rowwise() |>
  mutate(total = sum(c_across(everything()))) |> 
  ungroup() |> 
  count(total) |> 
  mutate(`p(X=x)` = n/sum(n))

library(ggplot2)

dist |> 
  ggplot() +
  aes(x = total, y = `p(X=x)`) +
  geom_col() +
  xlab("sum of dice (x)") +
  ylab("Probability of outcome, Pr(X=x)") +
  expand_limits(y = 0)

  
  

Figure C.4: Distribution of the sum of five dice

In comparison, the outcome of just one die is not bell-shaped (Figure C.5).

library(dplyr)
dist = 
  expand.grid(1:6) |> 
  rowwise() |>
  mutate(total = sum(c_across(everything()))) |> 
  ungroup() |> 
  count(total) |> 
  mutate(`p(X=x)` = n/sum(n))

library(ggplot2)

dist |> 
  ggplot() +
  aes(x = total, y = `p(X=x)`) +
  geom_col() +
  xlab("sum of dice (x)") +
  ylab("Probability of outcome, Pr(X=x)") +
  expand_limits(y = 0)

  
  

Figure C.5: Distribution of the outcome of one die

What distribution does a single die have?

Answer: discrete uniform on 1:6.

C.6 Additional resources

• Miller (2017)

Dobson, Annette J, and Adrian G Barnett. 2018. An Introduction to Generalized Linear Models. 4th ed. CRC press. https://doi.org/10.1201/9781315182780.

Kalbfleisch, John D, and Ross L Prentice. 2011. The Statistical Analysis of Failure Time Data. John Wiley & Sons.

Klein, John P, and Melvin L Moeschberger. 2003. Survival Analysis: Techniques for Censored and Truncated Data. Vol. 1230. Springer. https://link.springer.com/book/10.1007/b97377.

Kleinbaum, David G, and Mitchel Klein. 2012. Survival Analysis: A Self-Learning Text. 3rd ed. Springer. https://link.springer.com/book/10.1007/978-1-4419-6646-9.

Miller, Steven J. 2017. The Probability Lifesaver : All the Tools You Need to Understand Chance. A Princeton Lifesaver Study Guide. Princeton: Princeton University Press. https://press.princeton.edu/books/hardcover/9780691149547/the-probability-lifesaver.

Rothman, Kenneth J., Timothy L. Lash, Tyler J. VanderWeele, and Sebastien Haneuse. 2021. Modern Epidemiology. Fourth edition. Philadelphia: Wolters Kluwer.

Vittinghoff, Eric, David V Glidden, Stephen C Shiboski, and Charles E McCulloch. 2012. Regression Methods in Biostatistics: Linear, Logistic, Survival, and Repeated Measures Models. 2nd ed. Springer. https://doi.org/10.1007/978-1-4614-1353-0.

---

1. for example in Dobson and Barnett (2018), Vittinghoff et al. (2012), Klein and Moeschberger (2003), and Kleinbaum and Klein (2012)

2. for example, in Rothman et al. (2021) and Kalbfleisch and Prentice (2011)