rm(list =ls())# delete any data that's already loaded into Rconflicts_prefer(dplyr::filter)ggplot2::theme_set(ggplot2::theme_bw()+# ggplot2::labs(col = "") +ggplot2::theme( legend.position ="bottom", text =ggplot2::element_text(size =12, family ="serif")))knitr::opts_chunk$set(message =FALSE)options('digits'=6)panderOptions("big.mark", ",")pander::panderOptions("table.emphasize.rownames", FALSE)pander::panderOptions("table.split.table", Inf)conflicts_prefer(dplyr::filter)# use the `filter()` function from dplyr() by defaultlegend_text_size=9run_graphs=TRUE
This course is about generalized linear models (for non-Gaussian outcomes)
UC Davis STA 108 (“Applied Statistical Methods: Regression Analysis”) is a prerequisite for this course, so everyone here should have some understanding of linear regression already.
We will review linear regression to:
make sure everyone is caught up
to provide an epidemiological perspective on model interpretation.
2.1.2 Chapter overview
Section 2.2: how to interpret linear regression models
Section 2.3: how to estimate linear regression models
Section 2.4: how to quantify uncertainty about our estimates
Section 2.8: how to tell if your model is insufficiently complex
2.2 Understanding Gaussian Linear Regression Models
2.2.1 Motivating example: birthweights and gestational age
Suppose we want to learn about the distributions of birthweights (outcome\(Y\)) for (human) babies born at different gestational ages (covariate\(A\)) and with different chromosomal sexes (covariate\(S\)) (Dobson and Barnett (2018) Example 2.2.2).
plot1<-bw|>ggplot(aes( x =age, y =weight, shape =sex, col =sex))+theme_bw()+xlab("Gestational age (weeks)")+ylab("Birthweight (grams)")+theme(legend.position ="bottom")+# expand_limits(y = 0, x = 0) +geom_point(alpha =.7)print(plot1+facet_wrap(~sex))
Figure 2.1: birthweight data (Dobson and Barnett (2018) Example 2.2.2)
Data notation
Let’s define some notation to represent this data:
\(Y\): birthweight (measured in grams)
\(S\): chromosomal sex: “male” (XY) or “female” (XX)
\(A\): estimated gestational age at birth (measured in weeks).
Female is the reference level for the categorical variable \(S\) (chromosomal sex) and corresponding indicator variable \(M\) . The choice of a reference level is arbitrary and does not limit what we can do with the resulting model; it only makes it more computationally convenient to make inferences about comparisons involving that reference group.
\(M\) and \(F\) are called dummy variables; together, they are a numeric representation of the categorical variable \(S\). Dummy variables with values 0 and 1 are also called indicator variables. There are other ways to construct dummy variables, such as using the values -1 and 1 (see Dobson and Barnett (2018) §2.4 for details).
We don’t have enough data to model the distribution of birth weight separately for each combination of gestational age and sex, so let’s instead consider a (relatively) simple model for how that distribution varies with gestational age and sex:
\[
\begin{aligned}
Y|M,A &\ \sim_{\text{ciid}}\ N(\mu(M,A), \sigma^2)\\
\mu(m,a) &= \beta_0 + \beta_M m + \beta_A a
\end{aligned}
\tag{2.1}\]
Table 2.3 shows the parameter estimates from R. Figure 2.2 shows the estimated model, superimposed on the data.
Show R code
bw_lm1<-lm( formula =weight~sex+age, data =bw)library(parameters)bw_lm1|>parameters::parameters()|>parameters::print_md( include_reference =include_reference_lines, select ="{estimate}")
Table 2.3: Regression parameter estimates for Model 2.1 of birthweight data
pred_female<-coef(bw_lm1)["(Intercept)"]+coef(bw_lm1)["age"]*36### or using built-in prediction:pred_female_alt<-predict(bw_lm1, newdata =tibble(sex ="female", age =36))
Age cancels out in this difference. In other words, according to this model, the difference between females and males with the same gestational age is the same for every age.
This characteristic is an assumption of the model specified by Equation 2.1. It’s hardwired into the parametric model structure, even before we estimated values for those parameters.
\(\beta_A\) is the slope of mean birthweight with respect to gestational age, adjusting for sex.
Or we can plug in the definition of slope:
\[\beta_A = E[Y|M = m, A = a+1] - E[Y|M = m, A = a]\]
Exchangeability and consistency have not been assessed; so we are not discussing potential outcomes (causality), only observed outcomes.
Exercise 2.5 What is the interpretation of \(\beta_M\) in Model 2.1?
Solution.
More precisely written: \[
\text{E}\left[Y|M=m,A=a\right] = \mu(m,a) = \bigg\{
\begin{matrix}
\beta_0 + \beta_M m +\beta_A a, & \text{for } m\in \left\{0,1\right\} \\
\text{undefined}, & \text{for } m \notin \left\{0,1\right\}
\end{matrix}
\] The model is undefined for \(m \notin \left\{0,1\right\}\), so the derivative with respect to \(m\) doesn’t exist.
Figure 2.3: Birthweight model with interaction term
Now we can see that the lines aren’t parallel.
Here’s another way we could rewrite this model (by collecting terms involving \(S\)):
\[
E[Y|M,A] = \beta_0 + \beta_M M+ (\beta_A + \beta_{AM} M) A
\]
If you want to understand a coefficient in a model with interactions, collect terms for the corresponding variable, and you will see which other covariates interact with the variable whose coefficient you are interested in. In this case, the association between \(A\) (age) varies between males and females (that is, by sex \(S\)). 4 So the slope of \(Y\) with respect to \(A\) depends on the value of \(M\). According to this model, there is no such thing as “the slope of birthweight with respect to age”. There are two slopes, one for each sex. We can only talk about “the slope of birthweight with respect to age among males” and “the slope of birthweight with respect to age among females”. Then: each non-interaction slope coefficient is the difference in means per unit difference in its corresponding variable, when all interacting variables are set to 0.
To learn what this model is assuming, let’s plug in a few values.
Exercise 2.7 According to this model, what’s the mean birthweight for a female born at 36 weeks?
Note that age now does show up in the difference: in other words, according to this model, the difference in mean birthweights between females and males with the same gestational age can vary by gestational age.
That’s how the lines in the graph ended up non-parallel.
Coefficient Interpretation
Exercise 2.10 What is the interpretation of \(\beta_{M}\) in Model 2.2?
Solution.
Mean birthweight among males with gestational age 0 weeks: \[
\begin{aligned}
\mu(1,0) &= \text{E}\left[Y|M = 1,A = 0\right]\\
&= \beta_0 + {\color{red}\beta_M} \cdot 1 + \beta_A \cdot 0 + \beta_{AM}\cdot 1 \cdot 0\\
&= \beta_0 + {\color{red}\beta_M}
\end{aligned}
\] Mean birthweight among females with gestational age 0 weeks: \[
\begin{aligned}
\mu(0,0) &= \text{E}\left[Y|M = 0,A = 0\right]\\
&= \beta_0 + {\color{red}\beta_M} \cdot 0 + \beta_A \cdot 0 + \beta_{AM}\cdot 0 \cdot 0\\
&= \beta_0
\end{aligned}
\]
\[
\begin{aligned}
\beta_{M} &= \mu(1,0) - \mu(0,0) \\
&= \text{E}\left[Y|M = 1,A = 0\right] - \text{E}\left[Y|M = 0,A = 0\right]
\end{aligned}
\]\(\beta_M\) is the difference in mean birthweight between males with gestational age 0 weeks and females with gestational age 0 weeks.
Exercise 2.11 What is the interpretation of \(\beta_{AM}\) in Model 2.2?
\[
\text{E}\left[Y|A=a, S=s\right] =
\beta_0 + \beta_A a + \beta_M m + \beta_{AM} (a \cdot m)
\]
In the stratified model, the intercept term \(\beta_0\) has been relabeled as \(\beta_F\).
Show R code
bw_lm2<-lm(weight~sex+age+sex:age, data =bw)bw_lm2|>parameters()|>print_md( include_reference =include_reference_lines, select ="{estimate}")
Table 2.6: Birthweight model with interaction term
Parameter
Estimate
(Intercept)
-2141.67
sex (male)
872.99
age
130.40
sex (male) × age
-18.42
Show R code
bw_lm_strat<-bw|>lm( formula =weight~sex+sex:age-1, data =_)bw_lm_strat|>parameters()|>print_md( select ="{estimate}")
Table 2.7: Birthweight model - stratified betas
Parameter
Estimate
sex (female)
-2141.67
sex (male)
-1268.67
sex (female) × age
130.40
sex (male) × age
111.98
2.2.6 Curved-line regression
If we transform some of our covariates (\(X\)s) and plot the resulting model on the original covariate scale, we end up with curved regression lines:
Show R code
bw_lm3<-lm(weight~sex:log(age)-1, data =bw)ggbw<-bw|>ggplot(aes(x =age, y =weight))+geom_point()+xlab("Gestational Age (weeks)")+ylab("Birth Weight (g)")ggbw2<-ggbw+stat_smooth( method ="lm", formula =y~log(x), geom ="smooth")+xlab("Gestational Age (weeks)")+ylab("Birth Weight (g)")ggbw2|>print()
Figure 2.4: birthweight model with age entering on log scale
Below is an example with a slightly more obvious curve.
Figure 2.5: palmerpenguins model with bill_length entering on log scale
2.3 Estimating Linear Models via Maximum Likelihood
In EPI 203 and our review of MLEs, we learned how to fit outcome-only models of the form \(p(X=x|\theta)\) to iid data \(\tilde{x}= (x_1,…,x_n)\) using maximum likelihood estimation.
Now, we apply the same procedure to linear regression models:
\(\ell_{\beta, \beta'} ''(\beta, \sigma^2;\mathbf X,\tilde{y})\) is negative definite at \(\beta = (\mathbf{X}'\mathbf{X})^{-1}X'y\), so \(\hat \beta_{ML} = (\mathbf{X}'\mathbf{X})^{-1}X'y\) is the MLE for \(\beta\).
Table 2.9: Estimated model for birthweight data with interaction term
Parameter
Coefficient
SE
95% CI
t(20)
p
(Intercept)
-2141.67
1163.60
(-4568.90, 285.56)
-1.84
0.081
sex (male)
872.99
1611.33
(-2488.18, 4234.17)
0.54
0.594
age
130.40
30.00
(67.82, 192.98)
4.35
< .001
sex (male) × age
-18.42
41.76
(-105.52, 68.68)
-0.44
0.664
So we can do confidence intervals, hypothesis tests, and p-values exactly as in the one-variable case we looked at previously.
2.3.6 Residual Standard Deviation
\(\hat \sigma\) represents an estimate of the Residual Standard Deviation parameter, \(\sigma\). We can extract \(\hat \sigma\) from the fitted model, using the sigma() function:
When we use likelihood ratio tests, we are comparing how well different models fit the data.
Likelihood ratio tests require “nested” models: one must be a special case of the other.
If we have non-nested models, we can instead use the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC):
AIC = \(-2 * \ell(\hat\theta) + 2 * p\)
BIC = \(-2 * \ell(\hat\theta) + p * \text{log}(n)\)
where \(\ell\) is the log-likelihood of the data evaluated using the parameter estimates \(\hat\theta\), \(p\) is the number of estimated parameters in the model (including \(\hat\sigma^2\)), and \(n\) is the number of observations.
You can calculate these criteria using the logLik() function, or use the built-in R functions:
AIC in R
Show R code
-2*logLik(bw_lm2)|>as.numeric()+2*(length(coef(bw_lm2))+1)# sigma counts as a parameter here#> [1] 323.159AIC(bw_lm2)#> [1] 323.159
For example, in the birthweight data, there are \(q = 12\) unique patterns (Table 2.10).
Show R code
bw_X_unique
Table 2.10: Unique covariate combinations in the birthweight data, with replicate counts
Definition 2.1 (Replicates) If a given covariate pattern has more than one observation in a dataset, those observations are called replicates.
Example 2.2 (Replicates in the birthweight data) In the birthweight dataset, there are 2 replicates of the combination “female, age 36” (Table 2.10).
Exercise 2.12 (Replicates in the birthweight data) Which covariate pattern(s) in the birthweight data has the most replicates?
Solution 2.1 (Replicates in the birthweight data). Two covariate patterns are tied for most replicates: males at age 40 weeks and females at age 40 weeks. 40 weeks is the usual length for human pregnancy (Polin, Fox, and Abman (2011)), so this result makes sense.
The likelihood ratio statistic for this test is \[\lambda = 2 * (\ell_{\text{full}} - \ell) = 10.355374\] where:
\(\ell_{\text{full}}\) is the log-likelihood of the full model: -151.401601
\(\ell\) is the log-likelihood of our comparison model (two slopes, two intercepts): -156.579288
This statistic is called the deviance or residual deviance for our two-slopes and two-intercepts model; it tells us how much the likelihood of that model deviates from the likelihood of the maximal model.
The corresponding p-value tells us whether there we have enough evidence to detect that our two-slopes, two-intercepts model is a worse fit for the data than the maximal model; in other words, it tells us if there’s evidence that we missed any important patterns. (Remember, a nonsignificant p-value could mean that we didn’t miss anything and a more complicated model is unnecessary, or it could mean we just don’t have enough data to tell the difference between these models.)
2.5.3 Null Deviance
Similarly, the least complicated model we could fit would have only one mean parameter, an intercept:
\[\text E[Y|X=x] = \beta_0\] We can fit this model in R like so:
The likelihood ratio statistic for the test comparing the null model to the maximal model is \[\lambda = 2 * (\ell_{\text{full}} - \ell_{0}) = 35.106732\] where:
\(\ell_{\text{0}}\) is the log-likelihood of the null model: -168.954967
\(\ell_{\text{full}}\) is the log-likelihood of the maximal model: -151.401601
This log-likelihood ratio statistic is called the null deviance. It tells us whether we have enough data to detect a difference between the null and full models.
Definition 2.2 (Predicted value) In a regression model \(\text{p}(y|\tilde{x})\), the predicted value of \(y\) given \(\tilde{x}\) is the estimated mean of \(Y\) given \(\tilde{X}=\tilde{x}\):
\[\hat y \stackrel{\text{def}}{=}\hat{\text{E}}\left[Y|\tilde{X}=\tilde{x}\right]\]
For linear models, the predicted value can be straightforwardly calculated by multiplying each predictor value \(x_j\) by its corresponding coefficient \(\beta_j\) and adding up the results:
These special predictions are called the fitted values of the dataset:
Definition 2.3 For a given dataset \((\tilde{Y}, \mathbf{X})\) and corresponding fitted model \(\text{p}_{\hat \beta}(\tilde{y}|\mathbf{x})\), the fitted value of \(y_i\) is the predicted value of \(y\) when \(\tilde{X}=\tilde{x}_i\) using the estimate parameters \(\hat \beta\).
bw_lm2|>predict(interval ="predict")|>head()#> Warning in predict.lm(bw_lm2, interval = "predict"): predictions on current data refer to _future_ responses#> fit lwr upr#> 1 2552.73 2124.50 2980.97#> 2 2552.73 2124.50 2980.97#> 3 2683.13 2275.99 3090.27#> 4 2813.53 2418.60 3208.47#> 5 2813.53 2418.60 3208.47#> 6 2943.93 2551.48 3336.38
The warning from the last command is: “predictions on current data refer to future responses” (since you already know what happened to the current data, and thus don’t need to predict it).
Figure 2.11: Birthweight model with interaction term
It’s not easy to assess these assumptions from this model. If there are multiple continuous covariates, it becomes even harder to visualize the raw data.
Fitted model for hers data
Consider the hers data from Vittinghoff et al. (2012).
The “heart and estrogen/progestin study” (HERS) was a clinical trial of hormone therapy for prevention of recurrent heart attacks and death among 2,763 post-menopausal women with existing coronary heart disease (CHD) (Hulley et al. 1998).
Maybe we can transform the data and model in some way to make it easier to inspect.
Definition 2.4 (Residual noise/deviation from the population mean) The residual noise in a probabilistic model \(p(Y)\), also known as the residual deviation of an observation from its population mean or residual for short, is the difference between an observed value \(y\) and its population mean:
We use the same notation for residual noise that we used for errors.
\(\text{E}\left[Y\right]\) can be viewed as an estimate of \(Y\), before \(y\) is observed. Conversely, each observation \(y\) can be viewed as an estimate of \(\text{E}\left[Y\right]\) (albeit an imprecise one, individually, since \(n=1\)).
We can rearrange Equation 2.10 to view \(y\) as the sum of its mean plus the residual noise:
Theorem 2.1 (Residuals in Gaussian models) If \(Y\) has a Gaussian distribution, then \(\varepsilon(Y)\) also has a Gaussian distribution, and vice versa.
Proof. Left to the reader.
Definition 2.5 (Residuals of a fitted model value) The residual of a fitted value \(\hat y\) (shorthand: “residual”) is its error relative to the observed data: \[
\begin{aligned}
e(\hat y) &\stackrel{\text{def}}{=}\varepsilon\left(\hat y\right)
\\&= y - \hat y
\end{aligned}
\]
Example 2.3 (residuals in birthweight data)
Show R code
plot1_interact+facet_wrap(~sex)+geom_segment(aes( x =age, y =predlm2, xend =age, yend =weight, col =sex, group =id), linetype ="dotted")
Figure 2.13: Fitted values and residuals for interaction model for birthweight data
Residuals of fitted values vs residual noise
\(e(\hat y)\) can be seen as the maximum likelihood estimate of the residual noise:
\[
\begin{aligned}
e(\hat y) &= y - \hat y
\\ &= \hat\varepsilon_{ML}
\end{aligned}
\]
General characteristics of residuals
Theorem 2.2 If \(\hat{\text{E}}\left[Y\right]\) is an unbiased estimator of the mean \(\text{E}\left[Y\right]\), then:
With enough data and a correct model, the residuals will be approximately Guassian distributed, with variance \(\sigma^2\), which we can estimate using \(\hat\sigma^2\); that is:
Hence, with enough data and a correct model, the standardized residuals will be approximately standard Gaussian; that is,
\[
r_i \ \sim_{\text{iid}}\ N(0,1)
\]
2.8.4 Marginal distributions of residuals
To look for problems with our model, we can check whether the residuals \(e_i\) and standardized residuals \(r_i\) look like they have the distributions that they are supposed to have, according to the model.
These are not quite the same, because R is doing something more complicated and precise to get the standard errors. Let’s not worry about those details for now; the difference is pretty small in this case:
Figure 2.20: Marginal distribution of standardized residuals
This looks similar, although the scale of the x-axis got narrower, because we divided by \(\hat\sigma\) (roughly speaking).
Still hard to tell if the distribution is Gaussian.
2.8.5 QQ plot of standardized residuals
Another way to assess normality is the QQ plot of the standardized residuals versus normal quantiles:
Show R code
library(ggfortify)# needed to make ggplot2::autoplot() work for `lm` objectsqqplot_lm2_auto<-bw_lm2|>autoplot( which =2, # options are 1:6; can do multiple at once ncol =1)+theme_classic()print(qqplot_lm2_auto)
If the Gaussian model were correct, these points should follow the dotted line.
Fig 2.4 panel (c) in Dobson and Barnett (2018) is a little different; they didn’t specify how they produced it, but other statistical analysis systems do things differently from R.
Figure 2.21: birthweight model (Equation 2.2): residuals versus fitted values
If the model is correct, the blue line should stay flat and close to 0, and the cloud of dots should have the same vertical spread regardless of the fitted value.
If not, we probably need to change the functional form of linear component of the mean, \[\text{E}[Y|X=x] = \beta_0 + \beta_1 X_1 + ... + \beta_p X_p\]
Figure 2.29: Scale-location plot of birthweight data
Here, the blue line doesn’t need to be near 0, but it should be flat. If not, the residual variance \(\sigma^2\) might not be constant, and we might need to transform our outcome \(Y\) (or use a model that allows non-constant variance).
Residuals versus leverage
We can also plot our standardized residuals against “leverage”, which roughly speaking is a measure of how unusual each \(x_i\) value is. Very unusual \(x_i\) values can have extreme effects on the model fit, so we might want to remove those observations as outliers, particularly if they have large residuals.
(adapted from Dobson and Barnett (2018) §6.3.3; for more information on prediction, see James et al. (2013) and Harrell (2015)).
If we have a lot of covariates in our dataset, we might want to choose a small subset to use in our model.
There are a few possible metrics to consider for choosing a “best” model.
2.9.1 Mean squared error
We might want to minimize the mean squared error, \(\text E[(y-\hat y)^2]\), for new observations that weren’t in our data set when we fit the model.
Unfortunately, \[\frac{1}{n}\sum_{i=1}^n (y_i-\hat y_i)^2\] gives a biased estimate of \(\text E[(y-\hat y)^2]\) for new data. If we want an unbiased estimate, we will have to be clever.
Cross-validation
Show R code
data("carbohydrate", package ="dobson")library(cvTools)full_model<-lm(carbohydrate~., data =carbohydrate)cv_full<-full_model|>cvFit( data =carbohydrate, K =5, R =10, y =carbohydrate$carbohydrate)reduced_model<-full_model|>update(formula =~.-age)cv_reduced<-reduced_model|>cvFit( data =carbohydrate, K =5, R =10, y =carbohydrate$carbohydrate)
Show R code
results_reduced<-tibble( model ="wgt+protein", errs =cv_reduced$reps[])results_full<-tibble( model ="wgt+age+protein", errs =cv_full$reps[])cv_results<-bind_rows(results_reduced, results_full)cv_results|>ggplot(aes(y =model, x =errs))+geom_boxplot()
coef(cvfit, s ="lambda.1se")#> 4 x 1 sparse Matrix of class "dgCMatrix"#> s0#> (Intercept) 33.88904273#> age -0.00429298#> weight -0.14803505#> protein 1.27651311
2.10 Categorical covariates with more than two levels
2.10.1 Example: birthweight
In the birthweight example, the variable sex had only two observed values:
Show R code
unique(bw$sex)#> [1] female male #> Levels: female male
If there are more than two observed values, we can’t just use a single variable with 0s and 1s.
2.10.2
For example, Table 2.16 shows the (in)famousiris data (Anderson (1935)), and Table 2.17 provides summary statistics. The data include three species: “setosa”, “versicolor”, and “virginica”.
If we want to model Sepal.Length by species, we could create a variable \(X\) that represents “setosa” as \(X=1\), “virginica” as \(X=2\), and “versicolor” as \(X=3\).
Show R code
data(iris)# this step is not always necessary, but ensures you're starting# from the original version of a dataset stored in a loaded packageiris<-iris|>tibble()|>mutate( X =case_when(Species=="setosa"~1,Species=="virginica"~2,Species=="versicolor"~3))iris|>distinct(Species, X)
Table 2.18: iris data with numeric coding of species
Harrell, Frank E. 2015. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. 2nd ed. Springer. https://doi.org/10.1007/978-3-319-19425-7.
Hogg, Robert V., Elliot A. Tanis, and Dale L. Zimmerman. 2015. Probability and Statistical Inference. Ninth edition. Boston: Pearson.
Hulley, Stephen, Deborah Grady, Trudy Bush, Curt Furberg, David Herrington, Betty Riggs, Eric Vittinghoff, for the Heart, and Estrogen/progestin Replacement Study (HERS) Research Group. 1998. “Randomized Trial of Estrogen Plus Progestin for Secondary Prevention of Coronary Heart Disease in Postmenopausal Women.”JAMA : The Journal of the American Medical Association 280 (7): 605–13.
James, Gareth, Daniela Witten, Trevor Hastie, Robert Tibshirani, et al. 2013. An Introduction to Statistical Learning. Vol. 112. Springer. https://www.statlearning.com/.
Vittinghoff, Eric, David V Glidden, Stephen C Shiboski, and Charles E McCulloch. 2012. Regression Methods in Biostatistics: Linear, Logistic, Survival, and Repeated Measures Models. 2nd ed. Springer. https://doi.org/10.1007/978-1-4614-1353-0.
Weisberg, Sanford. 2005. Applied Linear Regression. Vol. 528. John Wiley & Sons.
the current version of the first regression course I ever took↩︎
\(M\) is implicitly a deterministic function of \(S\)↩︎
\(F\) is implicitly a deterministic function of \(S\)↩︎
some call this kind of variation “interaction” or “effect modification”, but “act”, “effect”, “modify”, and “by” all suggest causality, which we are not prepared to assess here; let’s try to avoid using causal terms, unless we are constructing a causal model.↩︎
# Linear (Gaussian) Models---{{< include shared-config.qmd >}}```{r}include_reference_lines <-FALSE```---:::{.callout-note}This content is adapted from:- @dobson4e, Chapters 2-6- @dunn2018generalized, Chapters 2-3- @vittinghoff2e, Chapter 4There are numerous textbooks specifically for linear regression, including:- @kutner2005applied: used for UCLA Biostatistics MS level linear models class- @chatterjee2015regression: used for Stanford MS-level linear models class- @seber2012linear: used for UCLA Biostatistics PhD level linear models class and UC Davis STA 108.- @kleinbaum2014applied: same first author as @kleinbaum2010logistic and @kleinbaum2012survival- *Linear Models with R* [@Faraway2025-io]- *Applied Linear Regression* by Sanford Weisberg [@weisberg2005applied]For more recommendations, see the discussion on [Reddit](https://www.reddit.com/r/statistics/comments/qwgctl/q_books_on_applied_linear_modelsregression_for/).- see also <https://web.stanford.edu/class/stats191>^[the current version of the first regression course I ever took]:::## Overview### Why this course includes linear regression {.smaller}:::{.fragment .fade-in-then-semi-out}* This course is about *generalized linear models* (for non-Gaussian outcomes)::::::{.fragment .fade-in-then-semi-out}* UC Davis STA 108 ("Applied Statistical Methods: Regression Analysis") is a prerequisite for this course, so everyone here should have some understanding of linear regression already.::::::{.fragment .fade-in}* We will review linear regression to:- make sure everyone is caught up- to provide an epidemiological perspective on model interpretation.:::### Chapter overview* @sec-understand-LMs: how to interpret linear regression models* @sec-est-LMs: how to estimate linear regression models* @sec-infer-LMs: how to quantify uncertainty about our estimates* @sec-diagnose-LMs: how to tell if your model is insufficiently complex## Understanding Gaussian Linear Regression Models {#sec-understand-LMs}### Motivating example: birthweights and gestational age {.smaller}Suppose we want to learn about the distributions of birthweights (*outcome* $Y$) for (human) babies born at different gestational ages (*covariate* $A$) and with different chromosomal sexes (*covariate* $S$) (@dobson4e Example 2.2.2).### Dobson `birthweight` data {.smaller}::::: {.panel-tabset}#### Data as table```{r}#| label: tbl-birthweight-data1#| tbl-cap: "`birthweight` data (@dobson4e Example 2.2.2)"library(dobson)data("birthweight", package ="dobson")birthweight```#### Reshape data for graphing```{r}#| label: tbl-birthweight-data2#| tbl-cap: "`birthweight` data reshaped"library(tidyverse)bw <- birthweight |>pivot_longer(cols =everything(),names_to =c("sex", ".value"),names_sep ="s " ) |>rename(age =`gestational age`) |>mutate(id =row_number(),sex = sex |>case_match("boy"~"male","girl"~"female" ) |>factor(levels =c("female", "male")),male = sex =="male",female = sex =="female" )bw```#### 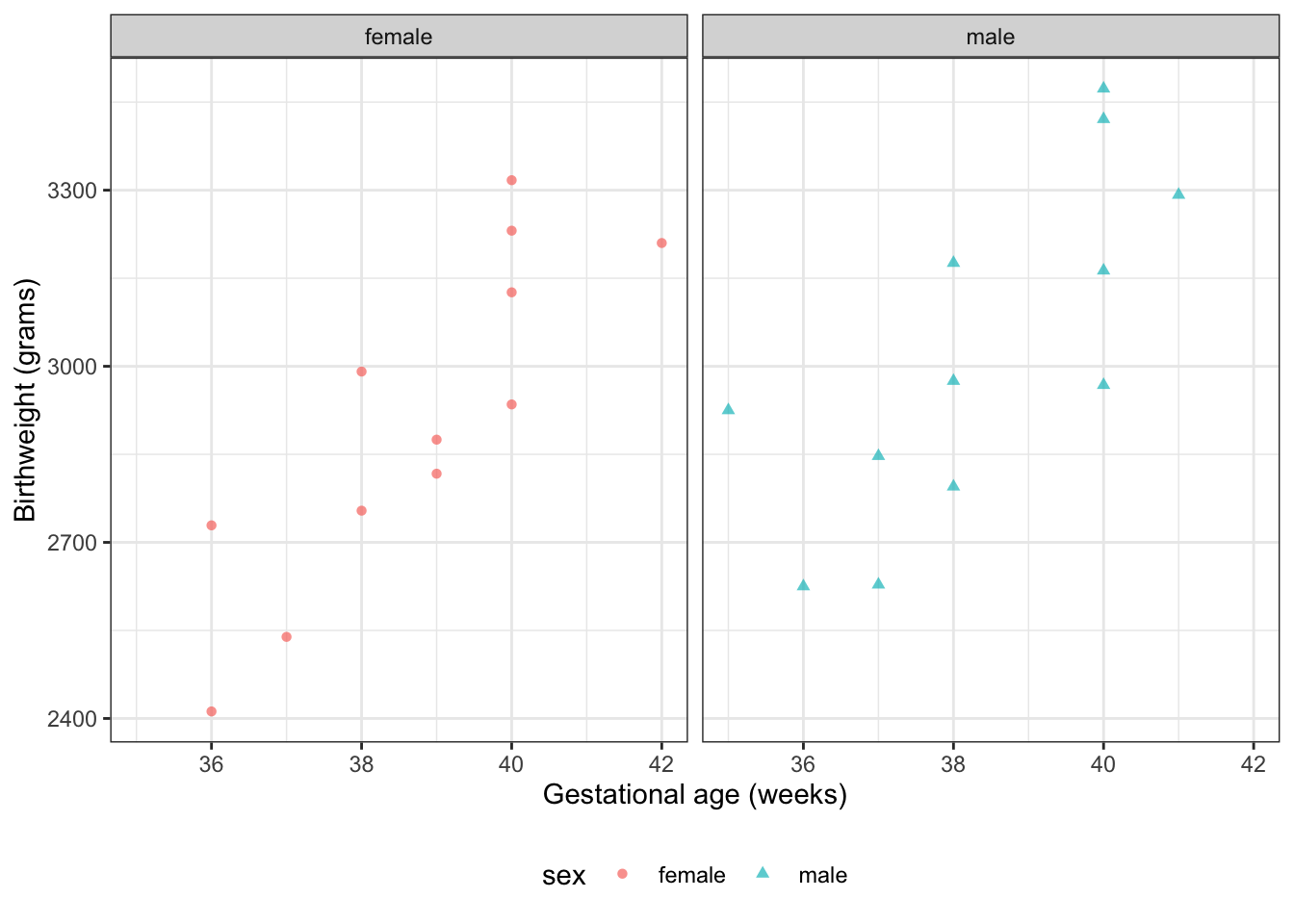Data as graph```{r}#| label: fig-plot-birthweight1#| fig-cap: "`birthweight` data (@dobson4e Example 2.2.2)"#| fig-height: 5#| fig-width: 7plot1 <- bw |>ggplot(aes(x = age,y = weight,shape = sex,col = sex )) +theme_bw() +xlab("Gestational age (weeks)") +ylab("Birthweight (grams)") +theme(legend.position ="bottom") +# expand_limits(y = 0, x = 0) +geom_point(alpha = .7)print(plot1 +facet_wrap(~sex))```:::::---#### Data notation {.smaller}::: notesLet's define some notation to represent this data::::- $Y$: birthweight (measured in grams)- $S$: chromosomal sex: "male" (XY) or "female" (XX)- $M$: indicator variable for $S$ = "male"^[$M$ is implicitly a deterministic function of $S$]- $M = 0$ if $S$ = "female"- $M = 1$ if $S$ = "male"- $F$: indicator variable for $S$ = "female"^[$F$ is implicitly a deterministic function of $S$]- $F = 1$ if $S$ = "female"- $F = 0$ if $S$ = "male"- $A$: estimated gestational age at birth (measured in weeks).::: notesFemale is the **reference level** for the categorical variable $S$ (chromosomal sex) and corresponding indicator variable $M$ . The choice of a reference level is arbitrary and does not limit what we can do with the resulting model; it only makes it more computationally convenient to make inferences about comparisons involving that reference group.$M$ and $F$ are called **dummy variables**; together, they are a numeric representation of the categorical variable $S$.Dummy variables with values 0 and 1 are also called **indicator variables**.There are other ways to construct dummy variables, such as using the values -1 and 1(see @dobson4e §2.4 for details).:::### Parallel lines regression {.smaller}(c.f. @dunn2018generalized [§2.10.3](https://link.springer.com/chapter/10.1007/978-1-4419-0118-7_2#Sec31))::: notesWe don't have enough data to model the distribution of birth weight separately for each combination of gestational age and sex, so let's instead consider a (relatively) simple model for how that distribution varies with gestational age and sex::::$$\baY|M,A &\sciid N(\mu(M,A), \sigma^2)\\\mu(m,a) &= \beta_0 + \beta_M m + \beta_A a\ea$$ {#eq-lm-parallel}:::{.notes}@tbl-lm-parallel shows the parameter estimates from R.@fig-parallel-fit1 shows the estimated model, superimposed on the data.:::::: {.column width=40%}::: {#tbl-lm-parallel}```{r}bw_lm1 <-lm(formula = weight ~ sex + age,data = bw)library(parameters)bw_lm1 |> parameters::parameters() |> parameters::print_md(include_reference = include_reference_lines,select ="{estimate}" )```Regression parameter estimates for [Model @eq-lm-parallel] of `birthweight` data:::::::::{.column width=10%}::::::{.column width=50%}:::{#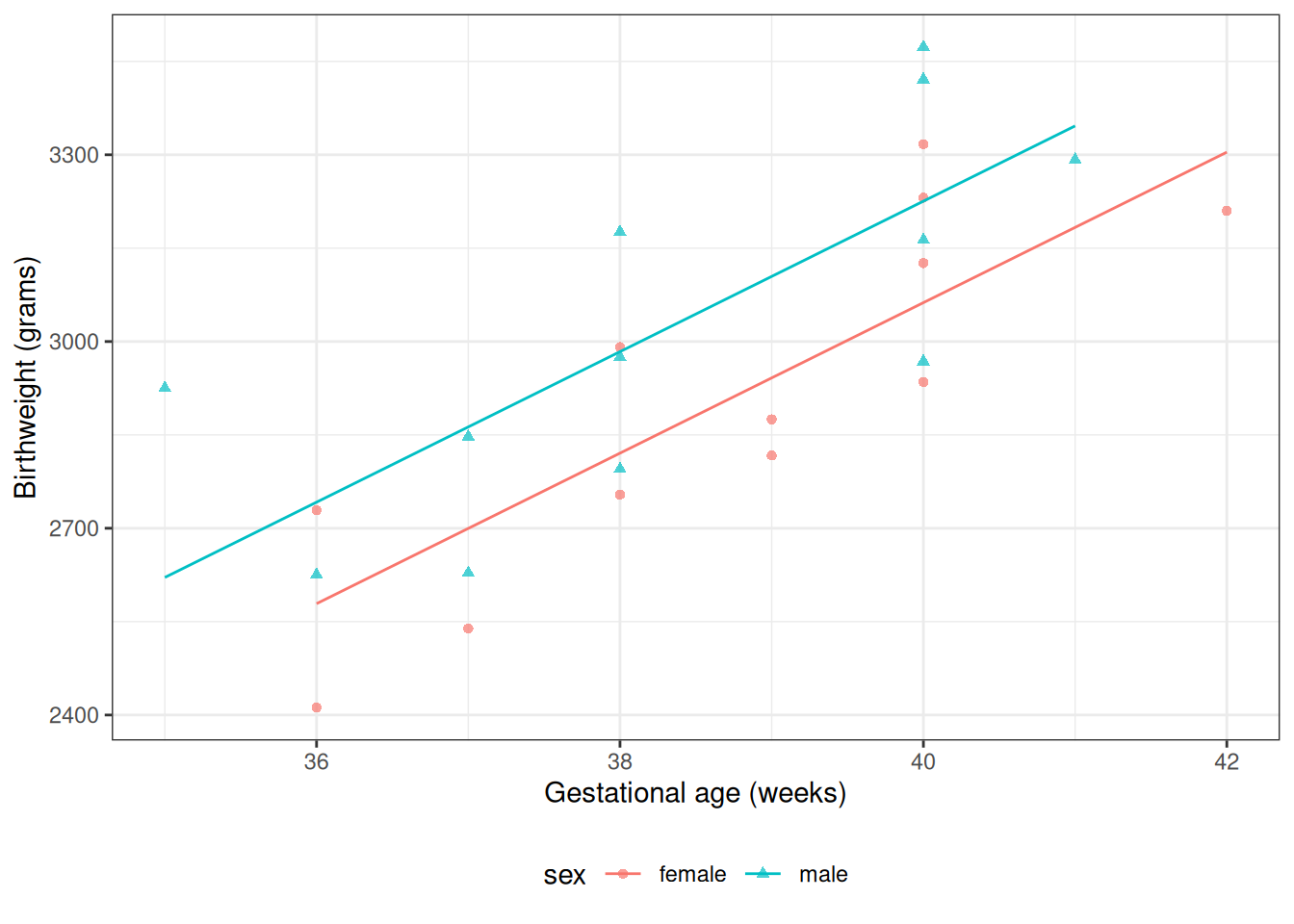fig-parallel-fit1}```{r}bw <- bw |>mutate(`E[Y|X=x]`=fitted(bw_lm1)) |>arrange(sex, age)plot2 <- plot1 %+% bw +geom_line(aes(y =`E[Y|X=x]`))print(plot2)```Graph of [Model @eq-lm-parallel] for `birthweight` data::::::---#### Model assumptions and predictions::: notesTo learn what this model is assuming, let's plug in a few values.:::---::: {#exr-pred-fem-parallel}What's the mean birthweight for a female born at 36 weeks?```{r}#| tbl-cap: "Estimated coefficients for [model @eq-lm-parallel]"#| code-fold: false#| echo: falsebw_lm1 |> parameters::parameters() |> parameters::print_md(select ="{estimate}" )```:::---:::{.solution .smaller}\ ```{r}#| tbl-cap: "Estimated coefficients for [model @eq-lm-parallel]"#| code-fold: false#| echo: falsebw_lm1 |> parameters::parameters() |> parameters::print_md(select ="{estimate}" )``````{r}pred_female <-coef(bw_lm1)["(Intercept)"] +coef(bw_lm1)["age"] *36### or using built-in prediction:pred_female_alt <-predict(bw_lm1, newdata =tibble(sex ="female", age =36))```$$\baE[Y|M = 0, A = 36]&= \beta_0 + \paren{\beta_M \cdot 0}+ \paren{\beta_A \cdot 36} \\&= `r coef(bw_lm1)["(Intercept)"]` + \paren{`r coef(bw_lm1)["sexmale"]` \cdot 0} + \paren{`r coef(bw_lm1)["age"]` \cdot 36} \\&= `r pred_female`\ea$$:::---:::{#exr-pred-male-parallel}What's the mean birthweight for a male born at 36 weeks?```{r}#| tbl-cap: "Estimated coefficients for [model @eq-lm-parallel]"#| code-fold: false#| echo: falsebw_lm1 |> parameters::parameters() |> parameters::print_md(select ="{estimate}" )```:::---:::{.solution}\ ```{r}#| tbl-cap: "Estimated coefficients for [model @eq-lm-parallel]"#| code-fold: false#| echo: falsebw_lm1 |> parameters::parameters() |> parameters::print_md(select ="{estimate}" )``````{r}pred_male <-coef(bw_lm1)["(Intercept)"] +coef(bw_lm1)["sexmale"] +coef(bw_lm1)["age"] *36```$$\baE[Y|M = 1, A = 36]&= \beta_0 + \beta_M \cdot 1+ \beta_A \cdot 36 \\&= `r pred_male`\ea$$:::---:::{#exr-diff-sex-parallel-1}What's the difference in mean birthweights between males born at 36 weeks and females born at 36 weeks?:::```{r}coef(bw_lm1)```---:::{.solution}$$\begin{aligned}& E[Y|M = 1, A = 36] - E[Y|M = 0, A = 36]\\&= `r pred_male` - `r pred_female`\\&=`r pred_male - pred_female`\end{aligned}$$Shortcut:$$\begin{aligned}& E[Y|M = 1, A = 36] - E[Y|M = 0, A = 36]\\&= (\beta_0 + \beta_M \cdot 1+ \beta_A \cdot 36) - (\beta_0 + \beta_M \cdot 0+ \beta_A \cdot 36) \\&= \beta_M \\&= `r coef(bw_lm1)["sexmale"]`\end{aligned}$$::::::{.notes}Age cancels out in this difference.In other words, according to this model, the difference between females and males with the same gestational age is the same for every age.This characteristic is an assumption of the modelspecified by @eq-lm-parallel.It's hardwired into the parametric model structure, even before we estimated values for those parameters.:::---#### Coefficient Interpretation{{< include _sec_linear_coef_interp_no_intxn.qmd >}}### 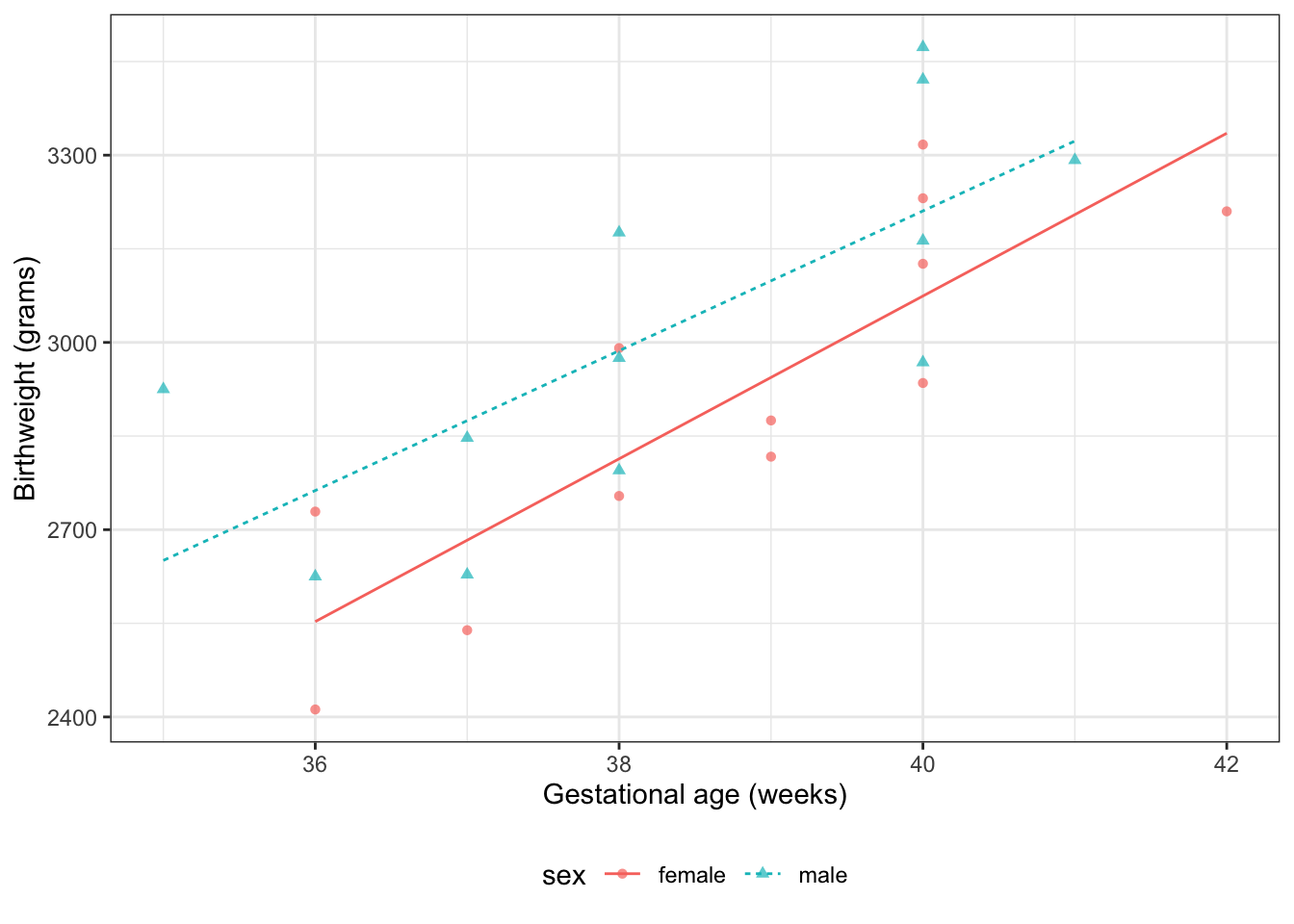Interactions {.smaller}::: notesWhat if we don't like that parallel lines assumption?Then we need to allow an "interaction" between age $A$ and sex $S$::::$$E[Y|S=s,A=a] = \beta_0 + \beta_A a+ \beta_M m + \beta_{AM} (a \cdot m)$$ {#eq-BW-lm-interact}::: notesNow, the slope of mean birthweight $E[Y|A,S]$ with respect to gestational age $A$ depends on the value of sex $S$.:::::: {.column width=40% .smaller}```{r}#| label: tbl-bw-model-coefs-interact#| tbl-cap: "Birthweight model with interaction term"bw_lm2 <-lm(weight ~ sex + age + sex:age, data = bw)bw_lm2 |>parameters() |> parameters::print_md(include_reference = include_reference_lines,select ="{estimate}" )```::::::{.column width=5%}::::::{.column width=55%}```{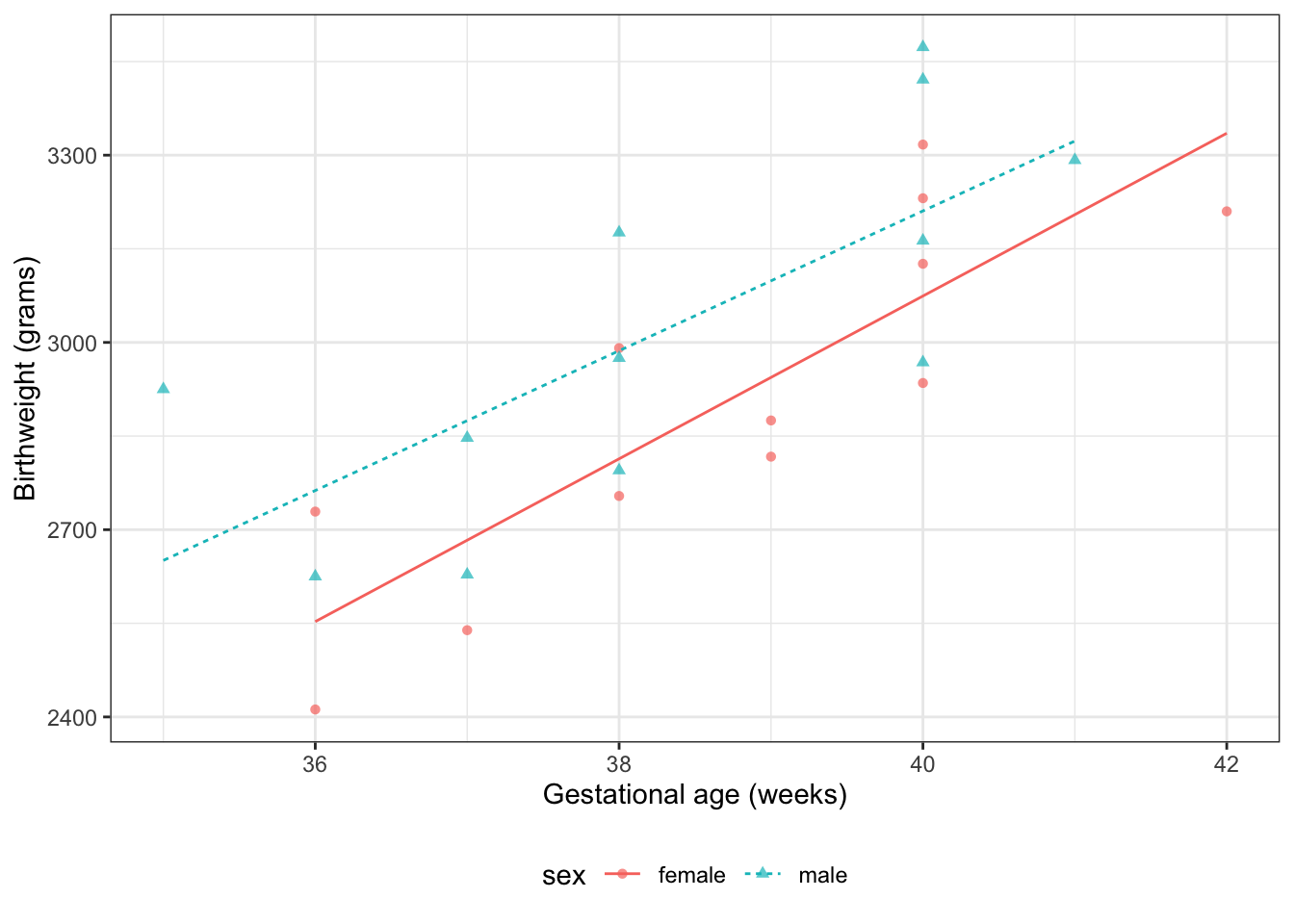r}#| label: fig-bw-interaction#| fig-cap: "Birthweight model with interaction term"bw <- bw |>mutate(predlm2 =predict(bw_lm2) ) |>arrange(sex, age)plot1_interact <- plot1 %+% bw +geom_line(aes(y = predlm2))print(plot1_interact)```:::::: {.notes}Now we can see that the lines aren't parallel.:::---Here's another way we could rewrite this model (by collecting terms involving $S$):$$E[Y|M,A] = \beta_0 + \beta_M M+ (\beta_A + \beta_{AM} M) A$$::: notesIf you want to understand a coefficient in a model with interactions, collect terms for the corresponding variable, and you will see which other covariates interact with the variable whose coefficient you are interested in.In this case, the association between$A$ (age) varies between males and females (that is, by sex $S$).^[some call this kind of variation "interaction" or "effect modification",but "act", "effect", "modify", and "by" all suggest causality, which we are not prepared to assess here;let's try to avoid using causal terms, unless we are constructing a causal model.]So the slope of $Y$ with respect to $A$ depends on the value of $M$.According to this model, there is no such thing as "*the* slope of birthweight with respect to age". There are two slopes, one for each sex.We can only talk about "the slope of birthweight with respect to age among males" and "the slope of birthweight with respect to age among females".Then: each non-interaction slope coefficient is the difference in means per unit difference in its corresponding variable, when all interacting variables are set to 0.:::---::: notesTo learn what this model is assuming, let's plug in a few values.::::::{#exr-pred-fem-interact}According to this model, what's the mean birthweight for a female born at 36 weeks?:::```{r}#| code-fold: false#| echo: falsebw_lm2 |>parameters() |>print_md(include_reference = include_reference_lines,select ="{estimate}" )```---::: {.solution}\ ```{r}#| code-fold: false#| echo: falsebw_lm2 |>parameters() |>print_md(include_reference = include_reference_lines,select ="{estimate}" )``````{r}pred_female <-coef(bw_lm2)["(Intercept)"] +coef(bw_lm2)["age"] *36```$$E[Y|M = 0, X_2 = 36] = \beta_0 + \beta_M \cdot 0+ \beta_A \cdot 36 + \beta_{AM} \cdot (0 * 36) = `r pred_female`$$ :::---:::{#exr-pred-interact-male_36}What's the mean birthweight for a male born at 36 weeks?```{r}#| code-fold: false#| echo: falsebw_lm2 |>parameters() |>print_md(include_reference = include_reference_lines,select ="{estimate}" )```:::---::: solution\ ```{r}#| code-fold: false#| echo: falsebw_lm2 |>parameters() |>print_md(include_reference = include_reference_lines,select ="{estimate}" )``````{r}pred_male <-coef(bw_lm2)["(Intercept)"] +coef(bw_lm2)["sexmale"] +coef(bw_lm2)["age"] *36+coef(bw_lm2)["sexmale:age"] *36```$$\baE[Y|M = 1, X_2 = 36]&= \beta_0 + \beta_M \cdot 1+ \beta_A \cdot 36 + \beta_{AM} \cdot 1 \cdot 36\\&= `r pred_male`\ea$$:::---:::{#exr-diff-gender-interact}What's the difference in mean birthweights between males born at 36 weeks and females born at 36 weeks?:::---:::{.solution}$$\begin{aligned}& E[Y|M = 1, A = 36] - E[Y|M = 0, A = 36]\\&= (\beta_0 + \beta_M \cdot 1+ \beta_A \cdot 36 + \beta_{AM} \cdot 1 \cdot 36)\\&\ \ \ \ \ -(\beta_0 + \beta_M \cdot 0+ \beta_A \cdot 36 + \beta_{AM} \cdot 0 \cdot 36) \\&= \beta_{S} + \beta_{AM}\cdot 36\\&= `r pred_male - pred_female`\end{aligned}$$::::::{.notes}Note that age now does show up in the difference: in other words, according to this model, the difference in mean birthweights between females and males with the same gestational age can vary by gestational age.That's how the lines in the graph ended up non-parallel.:::---#### Coefficient Interpretation{{< include _sec_linear_coef_interp_intxn.qmd >}}--- #### Compare coefficient interpretations:::{#tbl-compare-coef-interps} $\mu(s,a)$ | $\beta_0 + \beta_M m + \beta_A a$ | $\beta_0 + \beta_M m + \beta_A a + \red{\beta_{AM} ma}$----------------|------------------------------------|--------------------------------------------------- $\beta_0$ | $E[Y\mid 1,a] - E[Y\mid 0,a]$ | $E[Y\mid 1,0] - E[Y\mid 0,0]$ $\beta_A$ | $\deriv{a}\mu(m,a)$ | $\deriv{a}\mu(0,a)$ $\beta_M$ | $E[Y\mid 1,a] - E[Y\mid 0,a]$ | $E[Y\mid 1,0] - E[Y\mid 0,0]$ $\beta_{AM}$ | | $\deriv{a}\mu(1,a) - \deriv{a}\mu(0,a)$Coefficient interpretations, by model structure:::### Stratified regression {.smaller}:::{.notes}We could re-write the interaction model as a stratified model, with a slope and intercept for each sex::::$$\E{Y|A=a, S=s} = \beta_M m + \beta_{AM} (a \cdot m) + \beta_F f + \beta_{AF} (a \cdot f)$$ {#eq-model-strat}Compare this stratified model (@eq-model-strat) with our interaction model, @eq-BW-lm-interact:$$\E{Y|A=a, S=s} = \beta_0 + \beta_A a + \beta_M m + \beta_{AM} (a \cdot m)$$::: notesIn the stratified model, the intercept term $\beta_0$ has been relabeled as $\beta_F$.:::::: {.column width=45%}```{r}#| label: tbl-bw-model-coefs-interact2#| tbl-cap: "Birthweight model with interaction term"bw_lm2 <-lm(weight ~ sex + age + sex:age, data = bw)bw_lm2 |>parameters() |>print_md(include_reference = include_reference_lines,select ="{estimate}" )```::::::{.column width=10%}::::::{.column width=45%}```{r}#| label: tbl-bw-model-coefs-strat#| tbl-cap: "Birthweight model - stratified betas"bw_lm_strat <- bw |>lm(formula = weight ~ sex + sex:age -1,data = _ )bw_lm_strat |>parameters() |>print_md(select ="{estimate}" )```:::### Curved-line regression::: notesIf we transform some of our covariates ($X$s) and plot the resulting model on the original covariate scale, we end up with curved regression lines::::```{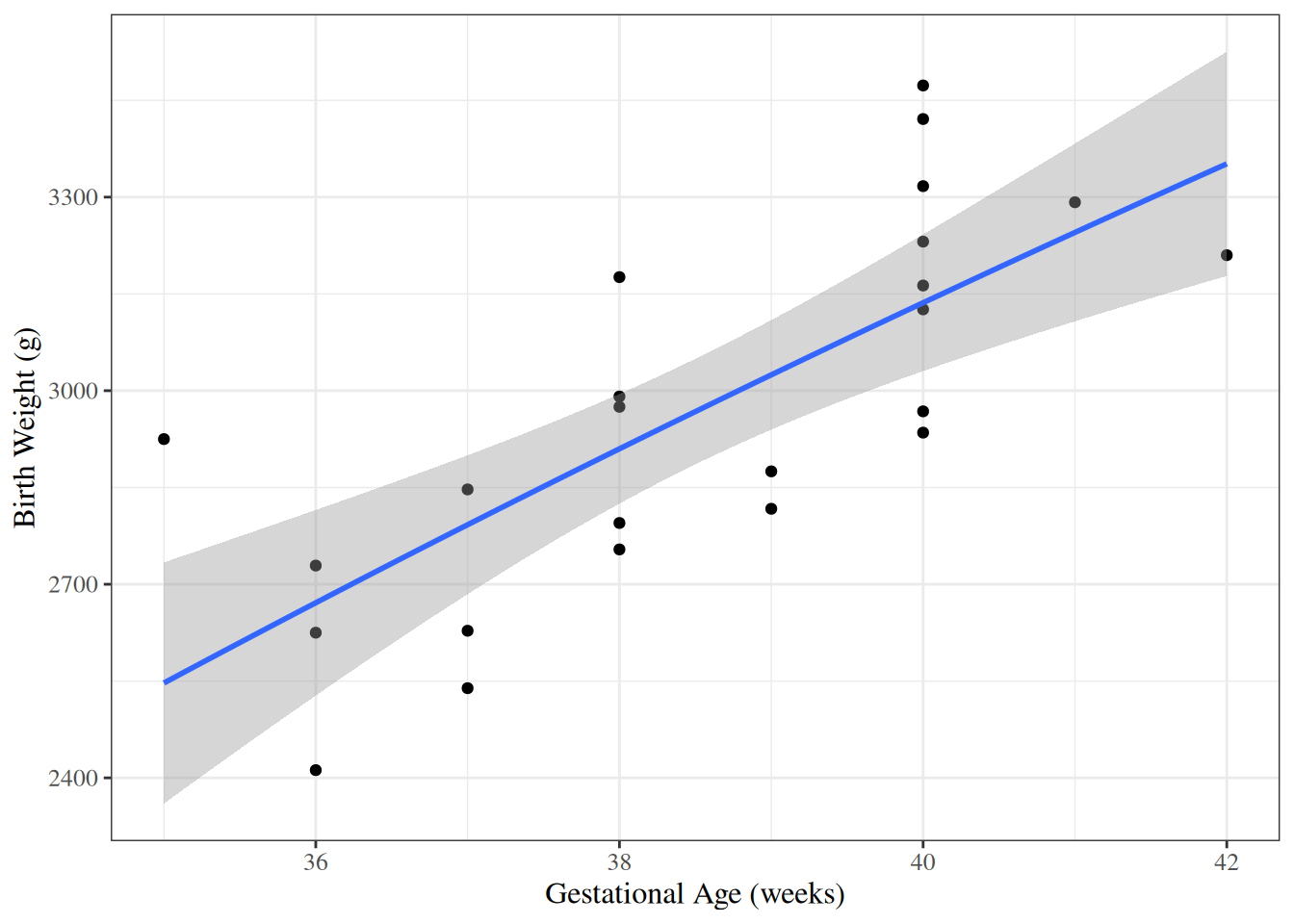r}#| label: fig-birthweight-log-x#| fig-cap: "`birthweight` model with `age` entering on log scale"bw_lm3 <-lm(weight ~ sex:log(age) -1, data = bw)ggbw <- bw |>ggplot(aes(x = age, y = weight) ) +geom_point() +xlab("Gestational Age (weeks)") +ylab("Birth Weight (g)")ggbw2 <- ggbw +stat_smooth(method ="lm",formula = y ~log(x),geom ="smooth" ) +xlab("Gestational Age (weeks)") +ylab("Birth Weight (g)")ggbw2 |>print()```---::: notesBelow is an example with a slightly more obvious curve.:::```{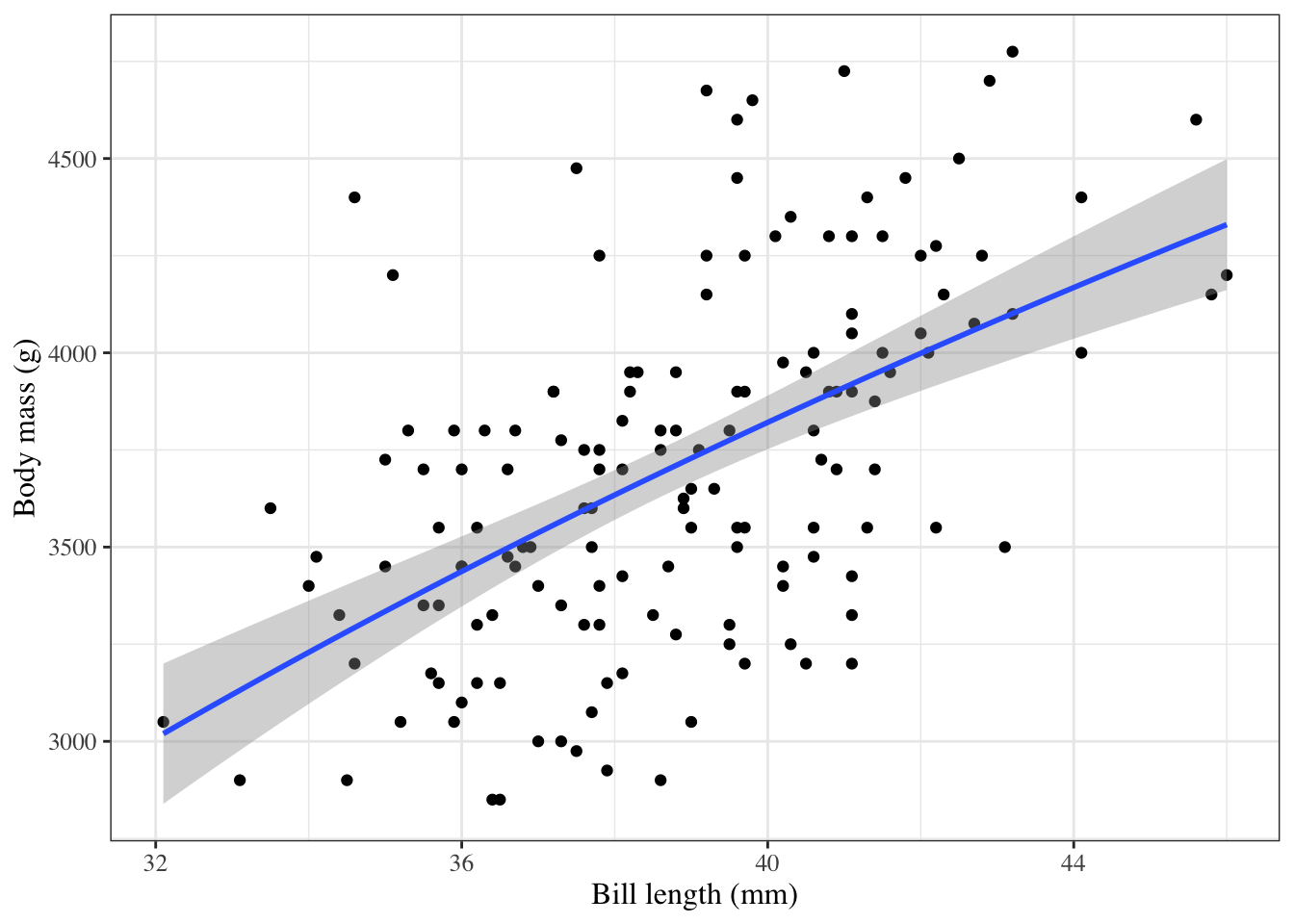r}#| label: fig-penguins-log-x#| fig-cap: "`palmerpenguins` model with `bill_length` entering on log scale"library(palmerpenguins)ggpenguins <- palmerpenguins::penguins |> dplyr::filter(species =="Adelie") |>ggplot(aes(x = bill_length_mm, y = body_mass_g) ) +geom_point() +xlab("Bill length (mm)") +ylab("Body mass (g)")ggpenguins2 <- ggpenguins +stat_smooth(method ="lm",formula = y ~log(x),geom ="smooth" ) +xlab("Bill length (mm)") +ylab("Body mass (g)")ggpenguins2 |>print()```## Estimating Linear Models via Maximum Likelihood {#sec-est-LMs}{{< include _sec_linreg_mle_est.qmd >}}---{{< include _sec_bw_vcov.qmd >}}## Inference about Gaussian Linear Regression Models {#sec-infer-LMs}### Motivating example: `birthweight` dataResearch question: is there really an interaction between sex and age?$H_0: \beta_{AM} = 0$$H_A: \beta_{AM} \neq 0$$P(|\hat\beta_{AM}| > |`r coef(bw_lm2)["sexmale:age"]`| \mid H_0)$ = ?### Wald tests and CIs {.smaller}R can give you Wald tests for single coefficients and corresponding CIs:```{r "wald tests bw_lm2"}bw_lm2 |>parameters() |>print_md(include_reference =TRUE )```To understand what's happening, let's replicate these results by hand for the interaction term.### P-values {.smaller}```{r}bw_lm2 |>parameters(keep ="sexmale:age") |>print_md(include_reference =TRUE )``````{r}beta_hat <-coef(summary(bw_lm2))["sexmale:age", "Estimate"]se_hat <-coef(summary(bw_lm2))["sexmale:age", "Std. Error"]dfresid <- bw_lm2$df.residualt_stat <-abs(beta_hat) / se_hatpval_t <-pt(-t_stat, df = dfresid, lower.tail =TRUE) +pt(t_stat, df = dfresid, lower.tail =FALSE)```$$\begin{aligned}&P\paren{| \hat \beta_{AM} | > |`r coef(bw_lm2)["sexmale:age"]`| \middle| H_0} \\&= \Pr \paren{\abs{ \frac{\hat\beta_{AM}}{\hat{SE}(\hat\beta_{AM})} } > \abs{ \frac{`r beta_hat`}{`r se_hat`} } \middle| H_0}\\&= \Pr \paren{\abs{ T_{`r dfresid`} } > `r t_stat` | H_0}\\&= `r pval_t`\end{aligned}$$ ::: notesThis matches the result in the table above.:::### Confidence intervals```{r}bw_lm2 |>parameters(keep ="sexmale:age") |>print_md(include_reference =TRUE )``````{r}#| label: confint-tq_t <-qt(p =0.975,df = dfresid,lower.tail =TRUE)q_t <-qt(p =0.025,df = dfresid,lower.tail =TRUE)confint_radius_t <- se_hat * q_tconfint_t <- beta_hat +c(-1, 1) * confint_radius_tprint(confint_t)```::: notesThis also matches.:::### Gaussian approximationsHere are the asymptotic (Gaussian approximation) equivalents:### P-values {.smaller}```{r}bw_lm2 |>parameters(keep ="sexmale:age") |>print_md(include_reference =TRUE )``````{r}pval_z <-pnorm(abs(t_stat), lower =FALSE) *2print(pval_z)```### Confidence intervals {.smaller}```{r}bw_lm2 |>parameters(keep ="sexmale:age") |>print_md(include_reference =TRUE )``````{r}confint_radius_z <- se_hat *qnorm(0.975, lower =TRUE)confint_z <- beta_hat +c(-1, 1) * confint_radius_zprint(confint_z)```### Likelihood ratio statistics```{r}logLik(bw_lm2)logLik(bw_lm1)log_LR <- (logLik(bw_lm2) -logLik(bw_lm1)) |>as.numeric()delta_df <- (bw_lm1$df.residual -df.residual(bw_lm2))x_max <-1```---```{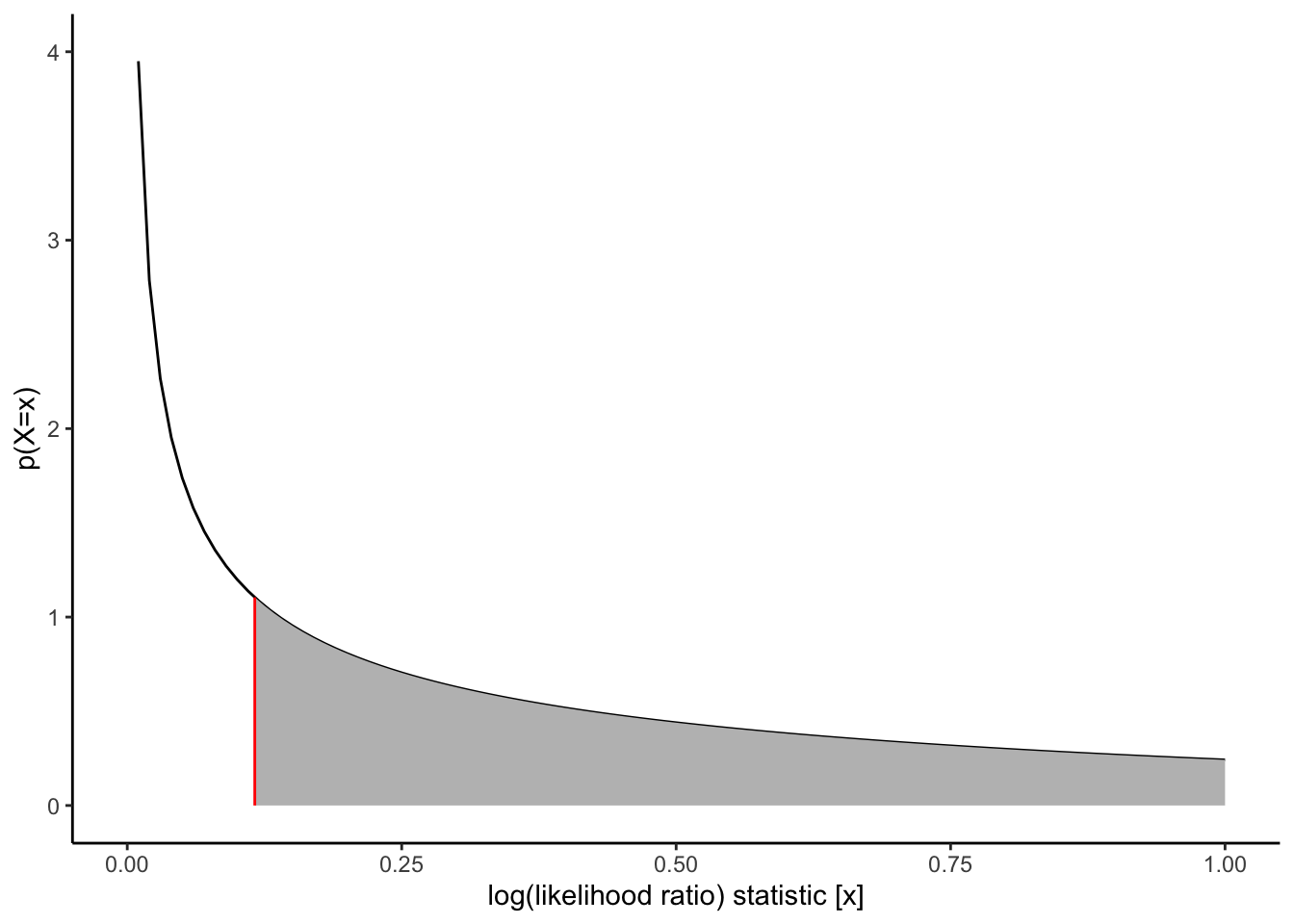r}#| label: fig-chisq-plot#| fig-cap: "Chi-square distribution"d_log_LR <-function(x, df = delta_df) dchisq(x, df = df)chisq_plot <-ggplot() +geom_function(fun = d_log_LR) +stat_function(fun = d_log_LR,xlim =c(log_LR, x_max),geom ="area",fill ="gray" ) +geom_segment(aes(x = log_LR,xend = log_LR,y =0,yend =d_log_LR(log_LR) ),col ="red" ) +xlim(0.0001, x_max) +ylim(0, 4) +ylab("p(X=x)") +xlab("log(likelihood ratio) statistic [x]") +theme_classic()chisq_plot |>print()```---Now we can get the p-value:```{r}#| label: LRT-pvalpchisq(q =2* log_LR,df = delta_df,lower =FALSE) |>print()```---In practice you don't have to do this by hand; there are functions to do it for you:```{r}# built inlibrary(lmtest)lrtest(bw_lm2, bw_lm1)```## Goodness of fit### AIC and BIC::: notesWhen we use likelihood ratio tests, we are comparing how well different models fit the data.Likelihood ratio tests require "nested" models: one must be a special case of the other.If we have non-nested models, we can instead use the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC)::::- AIC = $-2 * \ell(\hat\theta) + 2 * p$- BIC = $-2 * \ell(\hat\theta) + p * \text{log}(n)$where $\ell$ is the log-likelihood of the data evaluated using the parameter estimates $\hat\theta$, $p$ is the number of estimated parameters in the model (including $\hat\sigma^2$), and $n$ is the number of observations.You can calculate these criteria using the `logLik()` function, or use the built-in R functions:#### AIC in R```{r}-2*logLik(bw_lm2) |>as.numeric() +2* (length(coef(bw_lm2)) +1) # sigma counts as a parameter hereAIC(bw_lm2)```#### BIC in R```{r}-2*logLik(bw_lm2) |>as.numeric() + (length(coef(bw_lm2)) +1) *log(nobs(bw_lm2))BIC(bw_lm2)```Large values of AIC and BIC are worse than small values. There are no hypothesis tests or p-values associated with these criteria.### (Residual) DevianceLet $q$ be the number of distinct covariate combinations in a data set.```{r}bw_X_unique <- bw |>count(sex, age)n_unique_bw <-nrow(bw_X_unique)```For example, in the `birthweight` data, there are $q = `r n_unique_bw`$ unique patterns (@tbl-bw-x-combos).::: {#tbl-bw-x-combos}```{r}bw_X_unique```Unique covariate combinations in the `birthweight` data, with replicate counts:::---::: {#def-replicates}#### ReplicatesIf a given covariate pattern has more than one observation in a dataset, those observations are called **replicates**.:::---::: {#exm-replicate-bw}#### Replicates in the `birthweight` dataIn the `birthweight` dataset, there are 2 replicates of the combination "female, age 36" (@tbl-bw-x-combos).:::---::: {#exr-replicate-bw}#### Replicates in the `birthweight` dataWhich covariate pattern(s) in the `birthweight` data has the most replicates?:::---::: {#sol-replicate-bw}#### Replicates in the `birthweight` dataTwo covariate patterns are tied for most replicates: males at age 40 weeks and females at age 40 weeks.40 weeks is the usual length for human pregnancy (@polin2011fetal), so this result makes sense.```{r}bw_X_unique |> dplyr::filter(n ==max(n))```:::---#### Saturated models {.smaller}The most complicated model we could fit would have one parameter (a mean) for each covariate pattern, plus a variance parameter:```{r}#| label: tbl-bw-model-sat#| tbl-cap: "Saturated model for the `birthweight` data"lm_max <- bw |>mutate(age =factor(age)) |>lm(formula = weight ~ sex:age -1,data = _ )lm_max |>parameters() |>print_md()```We call this model the **full**, **maximal**, or **saturated** model for this dataset.---```{r}library(rlang) # defines the `.data` pronounplot_PIs_and_CIs <-function(model, data) { cis <- model |>predict(interval ="confidence") |>suppressWarnings() |> tibble::as_tibble()names(cis) <-paste("ci", names(cis), sep ="_") preds <- model |>predict(interval ="predict") |>suppressWarnings() |> tibble::as_tibble()names(preds) <-paste("pred", names(preds), sep ="_") dplyr::bind_cols(bw, cis, preds) |> ggplot2::ggplot() + ggplot2::aes(x = .data$age, y = .data$weight, col = .data$sex ) + ggplot2::geom_point() + ggplot2::theme(legend.position ="bottom") + ggplot2::geom_line(ggplot2::aes(y = .data$ci_fit)) + ggplot2::geom_ribbon( ggplot2::aes(ymin = .data$pred_lwr,ymax = .data$pred_upr ),alpha =0.2 ) + ggplot2::geom_ribbon( ggplot2::aes(ymin = .data$ci_lwr,ymax = .data$ci_upr ),alpha =0.5 ) + ggplot2::facet_wrap(~sex)}```:::{#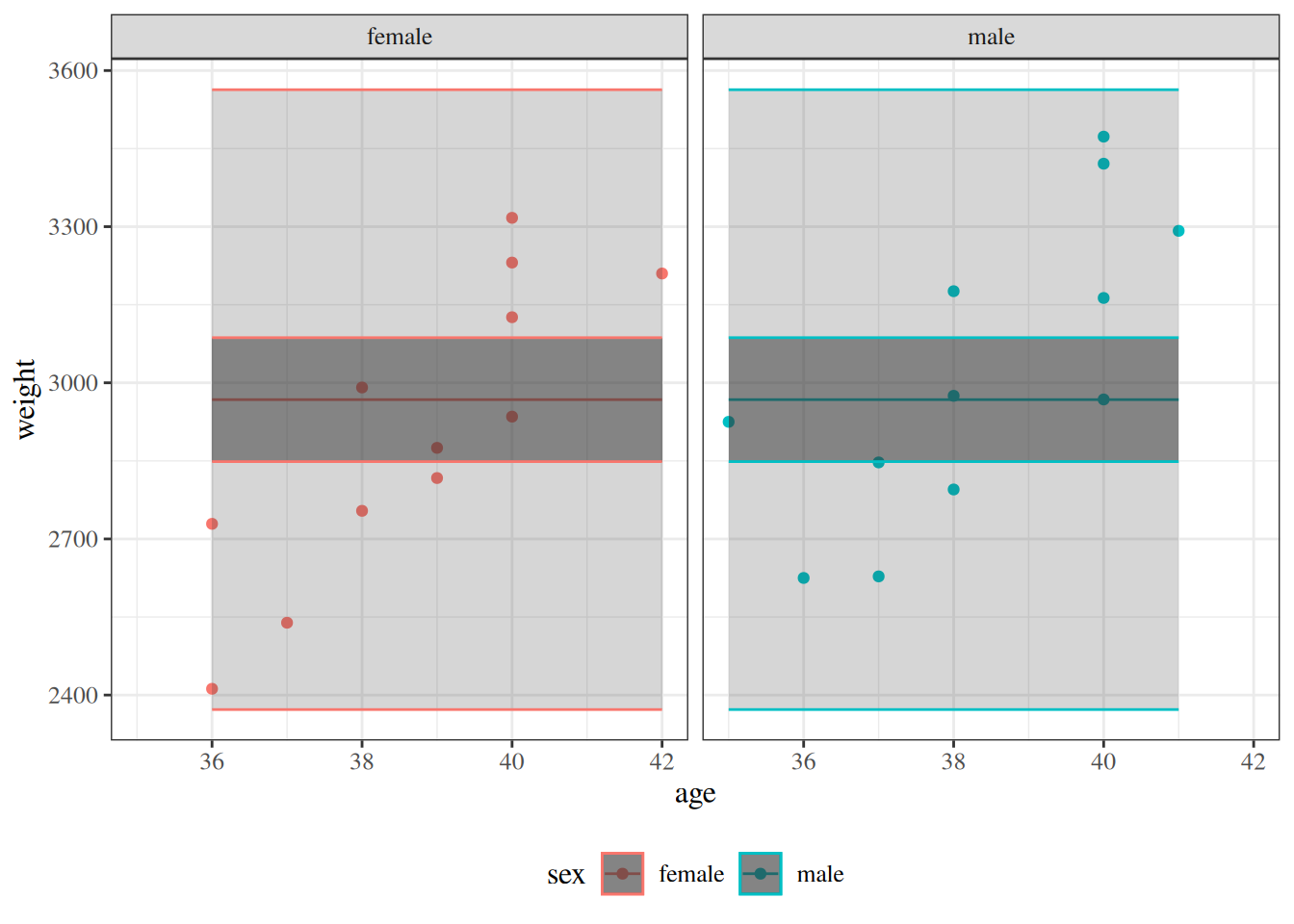fig-max-vs-intxn-fits layout-ncol=2}:::{#fig-fit-intxn}```{r}plot_PIs_and_CIs(bw_lm2, bw)```Model [-@eq-BW-lm-interact] (linear with age:sex interaction)::::::{#fig-fit-max}```{r}plot_PIs_and_CIs(lm_max, bw)```Saturated model:::Model [-@eq-BW-lm-interact] and saturated model for `birthweight` data, with confidence and prediction intervals:::---We can calculate the log-likelihood of this model as usual:```{r}logLik(lm_max)```We can compare this model to our other models using chi-square tests, as usual:```{r}lrtest(lm_max, bw_lm2)```The likelihood ratio statistic for this test is $$\lambda = 2 * (\ell_{\text{full}} - \ell) = `r 2 * (logLik(lm_max) - logLik(bw_lm2))`$$ where:- $\ell_{\text{full}}$ is the log-likelihood of the full model: `r logLik(lm_max)`- $\ell$ is the log-likelihood of our comparison model (two slopes, two intercepts): `r logLik(bw_lm2)`This statistic is called the **deviance** or **residual deviance** for our two-slopes and two-intercepts model; it tells us how much the likelihood of that model deviates from the likelihood of the maximal model.The corresponding p-value tells us whether there we have enough evidence to detect that our two-slopes, two-intercepts model is a worse fit for the data than the maximal model; in other words, it tells us if there's evidence that we missed any important patterns. (Remember, a nonsignificant p-value could mean that we didn't miss anything and a more complicated model is unnecessary, or it could mean we just don't have enough data to tell the difference between these models.)### Null DevianceSimilarly, the *least* complicated model we could fit would have only one mean parameter, an intercept:$$\text E[Y|X=x] = \beta_0$$ We can fit this model in R like so:```{r}lm0 <-lm(weight ~1, data = bw)lm0 |>parameters() |>print_md()```---:::{#fig-null-model}```{r}lm0 |>plot_PIs_and_CIs()```Null model for birthweight data, with 95% confidence and prediction intervals.:::---This model also has a likelihood:```{r}logLik(lm0)```And we can compare it to more complicated models using a likelihood ratio test:```{r}lrtest(bw_lm2, lm0)```The likelihood ratio statistic for the test comparing the null model to the maximal model is $$\lambda = 2 * (\ell_{\text{full}} - \ell_{0}) = `r 2 * (logLik(lm_max) - logLik(lm0))`$$ where:- $\ell_{\text{0}}$ is the log-likelihood of the null model: `r logLik(lm0)`- $\ell_{\text{full}}$ is the log-likelihood of the maximal model: `r logLik(lm_max)`In R, this test is:```{r}lrtest(lm_max, lm0)```This log-likelihood ratio statistic is called the **null deviance**. It tells us whether we have enough data to detect a difference between the null and full models.## Rescaling### Rescale age {.smaller}```{r}bw <- bw |>mutate(`age - mean`= age -mean(age),`age - 36wks`= age -36 )lm1_c <-lm(weight ~ sex +`age - 36wks`, data = bw)lm2_c <-lm(weight ~ sex +`age - 36wks`+ sex:`age - 36wks`, data = bw)parameters(lm2_c, ci_method ="wald") |>print_md()```Compare with what we got without rescaling:```{r}parameters(bw_lm2, ci_method ="wald") |>print_md()```## Prediction### Prediction for linear models:::{#def-predicted-value}#### Predicted valueIn a regression model $\p(y|\vx)$, the **predicted value** of $y$ given $\vx$ is the estimated mean of $Y$ given $\vX=\vx$:$$\hat y \eqdef \hE{Y|\vX=\vx}$$:::---For linear models, the predicted value can be straightforwardly calculated by multiplying each predictor value $x_j$ by its corresponding coefficient $\beta_j$ and adding up the results:$$\begin{aligned}\hat y &= \hE{Y|\vX=\vx} \\&= \vx'\hat\beta \\&= \hat\beta_0\cdot 1 + \hat\beta_1 x_1 + ... + \hat\beta_p x_p\end{aligned}$$---### Example: prediction for the `birthweight` data```{r}x <-c(1, 1, 40)sum(x *coef(bw_lm1))```R has built-in functions for prediction:```{r}x <-tibble(age =40, sex ="male")bw_lm1 |>predict(newdata = x)```If you don't provide `newdata`, R will use the covariate values from the original dataset:```{r}predict(bw_lm1)```These special predictions are called the *fitted values* of the dataset::::{#def-fitted-value}For a given dataset $(\vY, \mX)$ and corresponding fitted model $\p_{\hb}(\vy|\mx)$, the **fitted value** of $y_i$ is the predicted value of $y$ when $\vX=\vx_i$ using the estimate parameters $\hb$.:::R has an extra function to get these values:```{r}fitted(bw_lm1)```### Confidence intervals {#sec-se-fitted}Use `predict(se.fit = TRUE)` to compute SEs for predicted values:```{r}bw_lm1 |>predict(newdata = x,se.fit =TRUE )```The output of `predict.lm(se.fit = TRUE)` is a `list()`; you can extract the elements with `$` or `magrittr::use_series()`:```{r}library(magrittr)bw_lm1 |>predict(newdata = x,se.fit =TRUE ) |>use_series(se.fit)```---We can construct **confidence intervals** for $\E{Y|X=x}$ using the usual formula:$$\mu(\vx) \in \paren{\red{\hat{\mu}(\vx)} \pm \blue{\zeta_\alpha}}$$$$\blue{\zeta_\alpha} = t_{n-p}\paren{1-\frac{\alpha}{2}} * \hse{\hat{\mu}(\vx)}$$$$\red{\hat{\mu}(\vx)} = \vx \cdot \hb$$$$\se{\hat{\mu}(\vx)} = \sqrt{\Var{\hat{\mu}(\vx)}}$$$$\ba\Var{\hat{\mu}(\vx)} &= \Var{x'\hat{\beta}}\\&= x' \Var{\hat{\beta}} x\\&= x' \sigma^2(\mX'\mX)^{-1} x\\&= \sigma^2 x' (\mX'\mX)^{-1} x\\&= \sumin \sumjn x_i x_j \Covs{\hb_i}{\hb_j}\ea$$$$\hVar{\hat{\mu}(\vx)} = \hs^2 x' (\mX'\mX)^{-1} x$$```{R}bw_lm2 |>predict(newdata = x,interval ="confidence")```---:::{#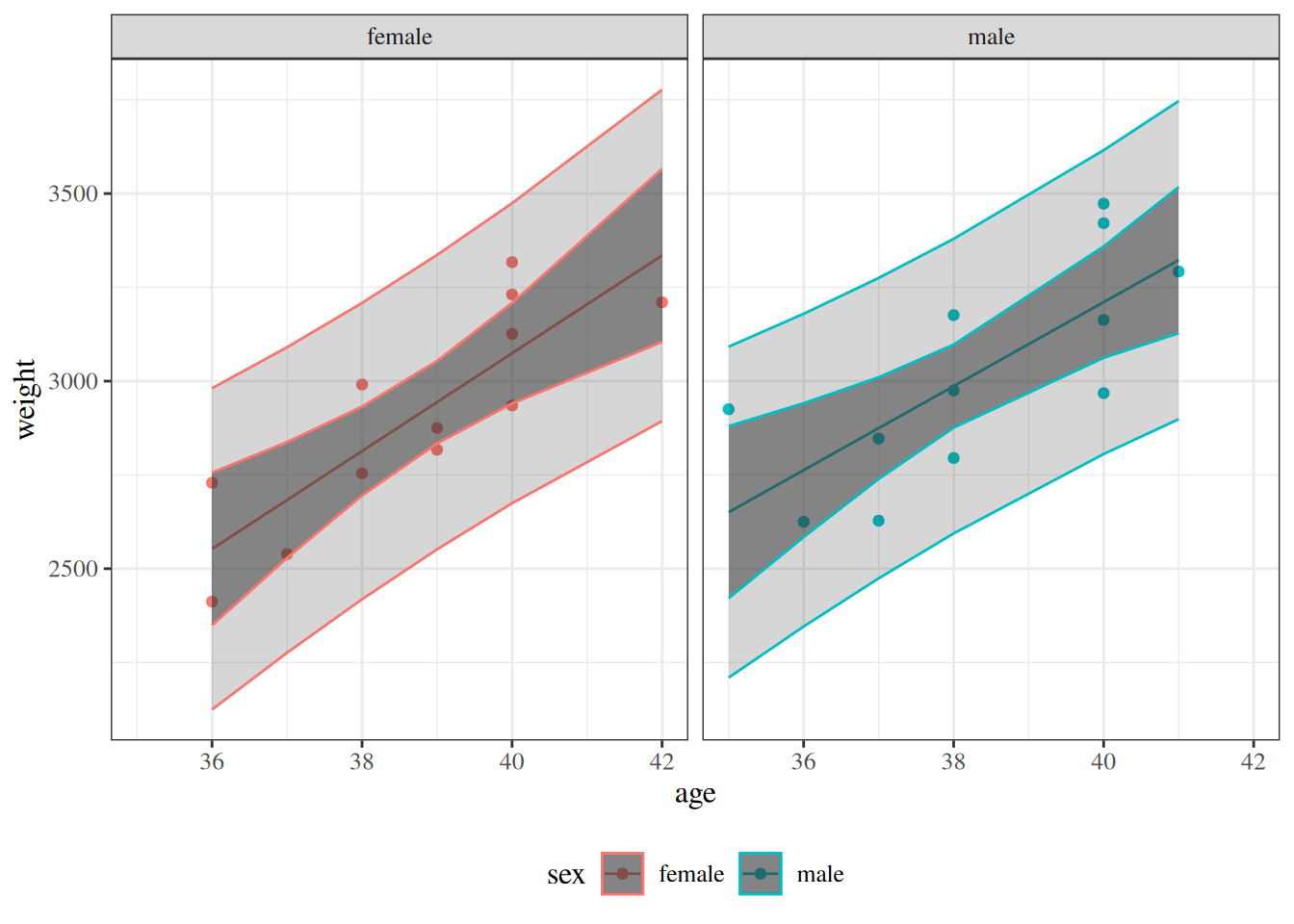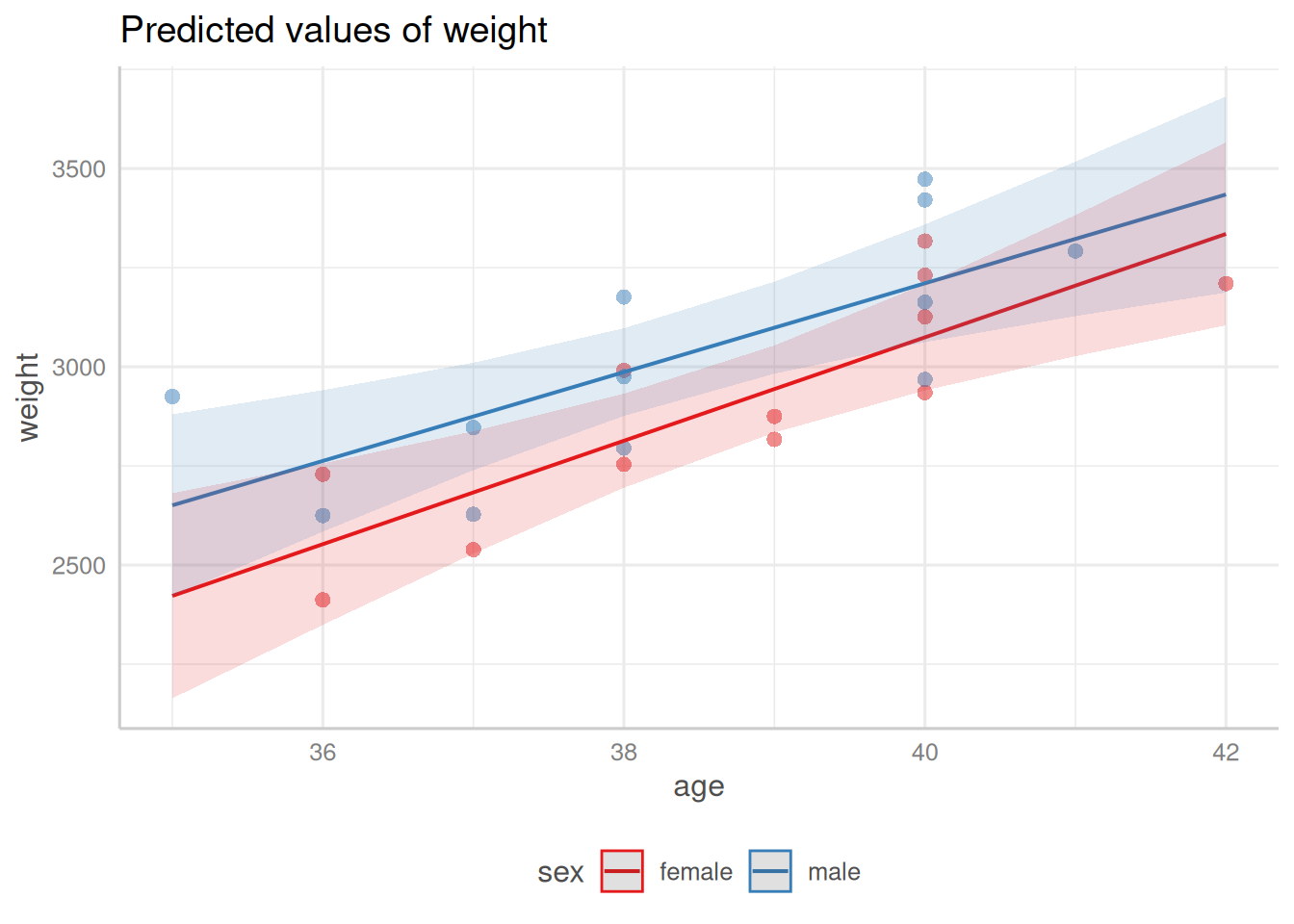fig-pred-int}```{r}library(sjPlot)bw_lm2 |>plot_model(type ="pred", terms =c("age", "sex"), show.data =TRUE) +theme_sjplot() +theme(legend.position ="bottom")```Predicted values and confidence bands for the `birthweight` model with interaction term:::### Prediction intervals {#sec-se-pred}We can also construct **prediction intervals** for the value of a new observation $Y^*$,given a covariate pattern $\vx^*$:$$\ba\hat{Y^*} &= \hat\mu({\vx}^*) + \hat{\epsilon}^*\\ \Var{\hat{Y}} &= \Var{\hat\mu} + \Var{\hat\epsilon}\\ \Var{\hat{Y}} &= \Var{x'\hb} + \Var{\hat\epsilon}\\ &= {{\vx}^{*\top}} \Var{\hb} {{\vx}^*} + \sigma^2\\ &= {{\vx}^{*\top}} \paren{\sigma^2(\mX'\mX)^{-1}} {{\vx}^*} + \sigma^2\\ &= \sigma^2 {{\vx}^{*\top}} (\mX'\mX)^{-1} {{\vx}^*} + \sigma^2\ea$${#eq-prediction-var}::: notesSee @hoggtanis2015 §7.6 (p. 340) for a longer version.:::```{r}#| code-fold: showbw_lm2 |>predict(newdata = x, interval ="predict")```---If you don't specify `newdata`, you get a warning:```{r}#| code-fold: show#| warning: truebw_lm2 |>predict(interval ="predict") |>head()```The warning from the last command is: "predictions on current data refer to *future* responses" (since you already know what happened to the current data, and thus don't need to predict it).See `?predict.lm` for more.---:::{#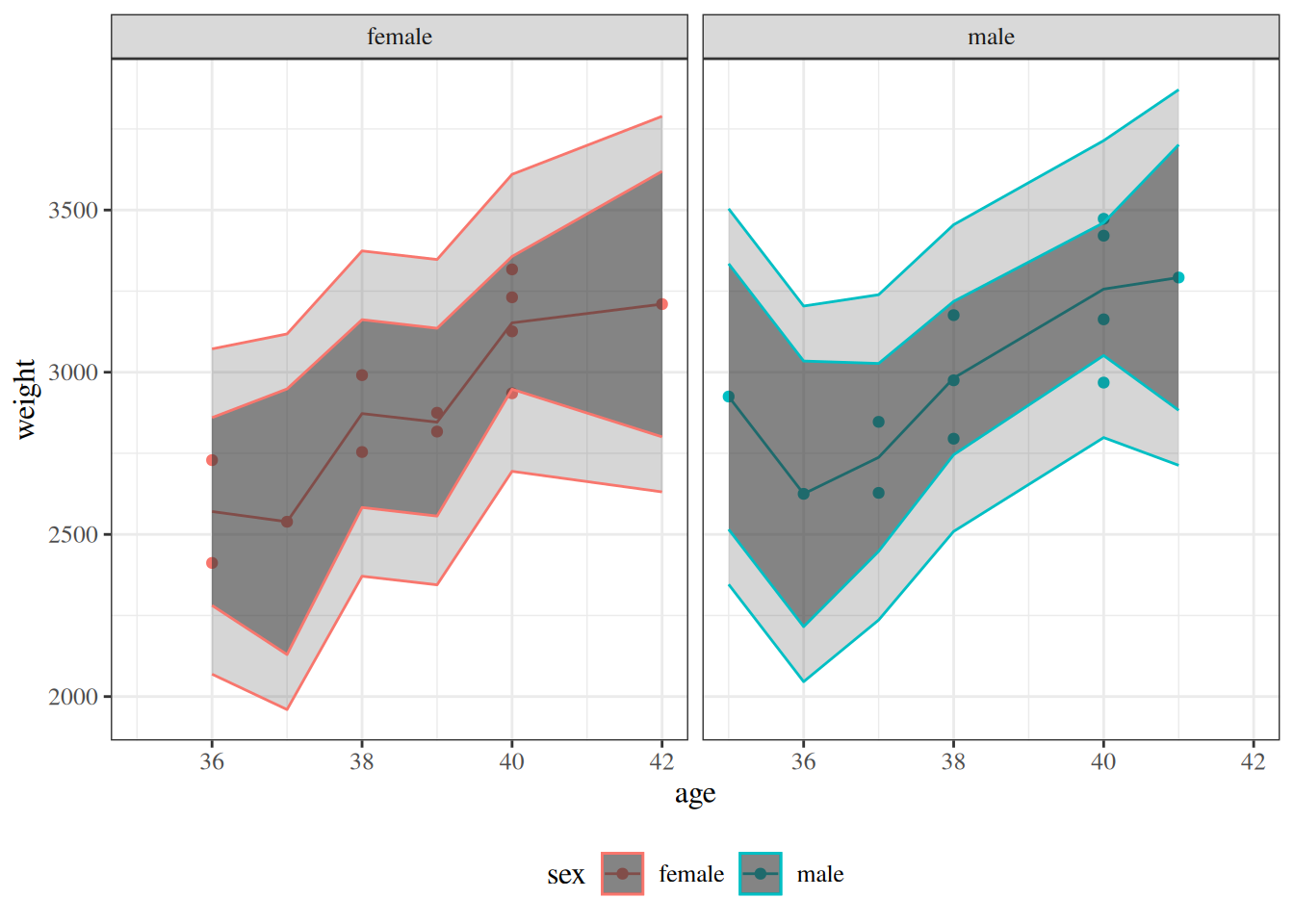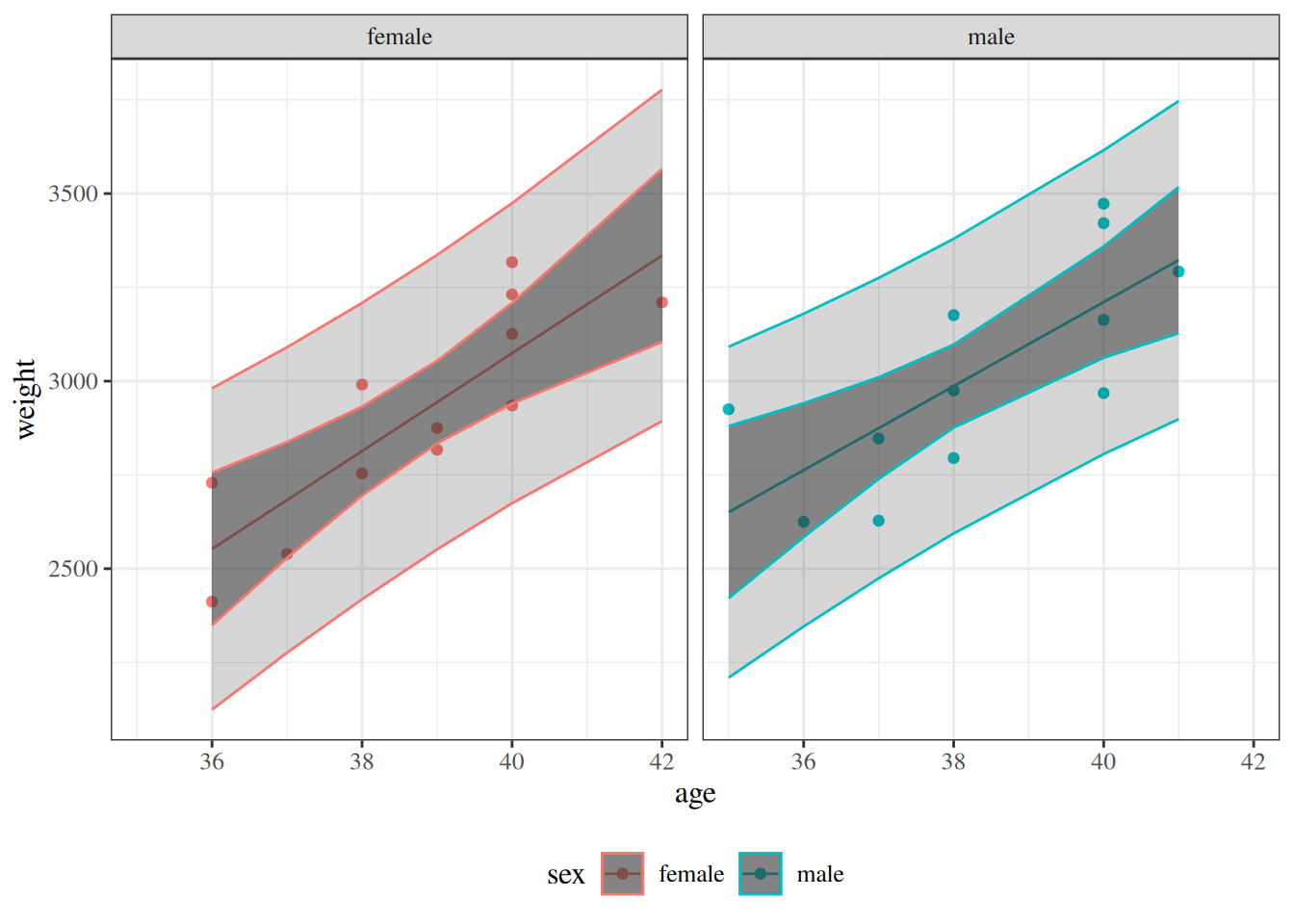fig-pred-int-bw}```{r}plot_PIs_and_CIs(bw_lm2, bw)```Confidence and prediction intervals for `birthweight` model [-@eq-BW-lm-interact]:::## Diagnostics {#sec-diagnose-LMs}:::{.callout-tip}This section is adapted from @dobson4e [§6.2-6.3] and @dunn2018generalized [Chapter 3](https://link.springer.com/chapter/10.1007/978-1-4419-0118-7_3).:::### Assumptions in linear regression models {.smaller .scrollable}{{< include _sec-linreg-assumptions.qmd >}}### Direct visualization::: notesThe most direct way to examine the fit of a model is to compare it to the raw observed data.:::```{r}#| label: fig-bw-interaction2#| fig-cap: "Birthweight model with interaction term"bw <- bw |>mutate(predlm2 =predict(bw_lm2) ) |>arrange(sex, age)plot1_interact <- plot1 %+% bw +geom_line(aes(y = predlm2))print(plot1_interact)```::: notesIt's not easy to assess these assumptions from this model.If there are multiple continuous covariates, it becomes even harder to visualize the raw data.:::---#### Fitted model for `hers` data {.smaller}::: notesConsider the `hers` data from @vittinghoff2e.{{< include _sec_hers_intro.qmd >}}::::::{#tbl-hers-data}```{r}hers <- fs::path_package("rme", "extdata/hersdata.dta") |> haven::read_dta()hers````hers` data:::---::: notesSuppose we consider models with and without intercept terms (i.e.,possibly forcing the intercept to go through 0)::::```{r}hers_lm_with_int <-lm(na.action = na.exclude, LDL ~ smoking * age, data = hers)library(equatiomatic)equatiomatic::extract_eq(hers_lm_with_int)``````{r}hers_lm_no_int <-lm(na.action = na.exclude, LDL ~ age + smoking:age -1, data = hers)library(equatiomatic)equatiomatic::extract_eq(hers_lm_no_int)```:::{#tbl-hers-maybe-int layout-ncol=2}:::{#tbl-hers-with-int}```{r}library(gtsummary)hers_lm_with_int |>tbl_regression(intercept =TRUE)```With intercept::::::{#tbl-hers-no-int}```{r}hers_lm_no_int |>tbl_regression(intercept =TRUE)```No intercept:::`hers` data models with and without intercepts:::---:::{#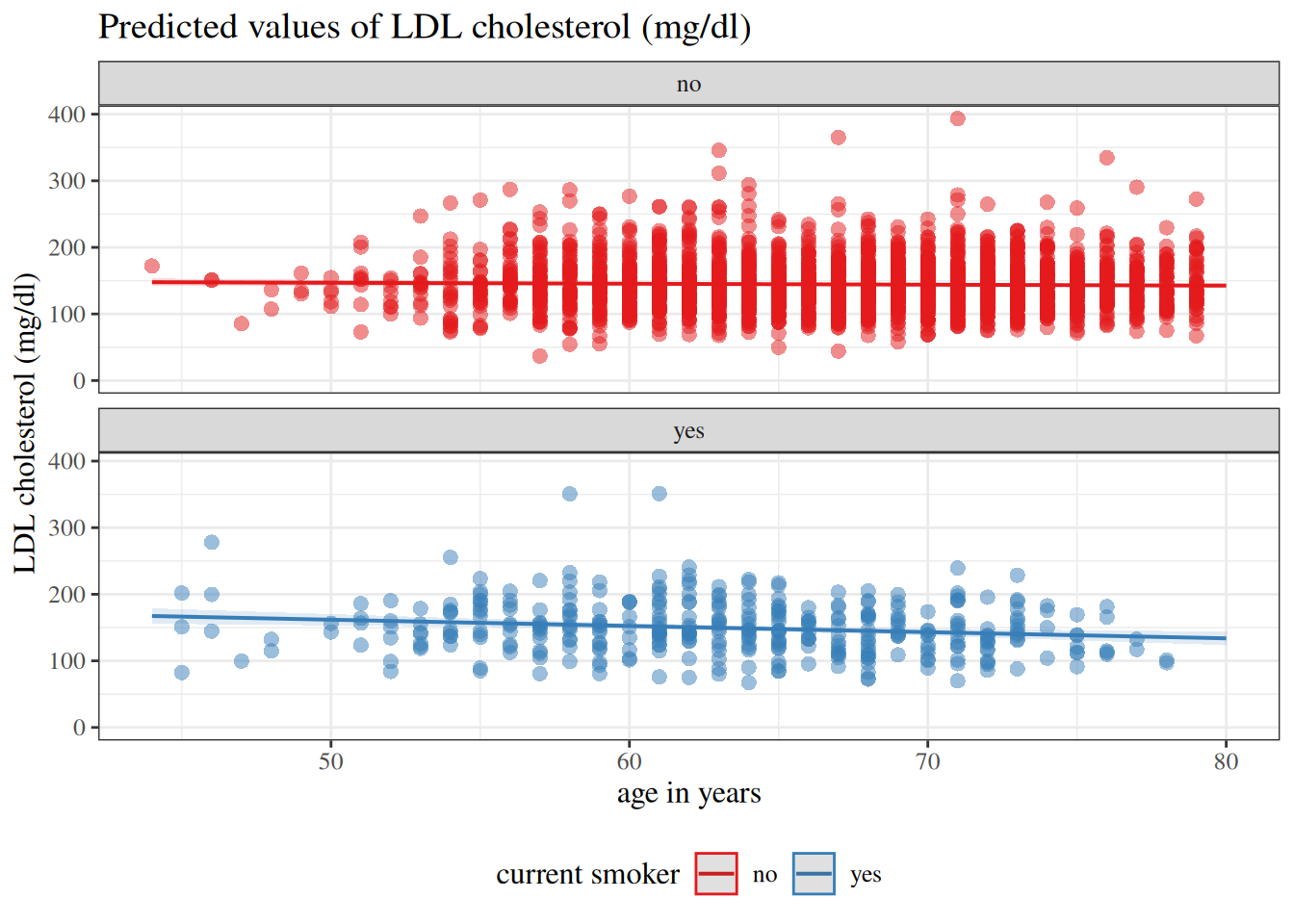fig-hers-maybe-int layout-ncol=2}:::{#fig-hers-no-int}```{r}library(sjPlot)hers_plot1 <- hers_lm_no_int |> sjPlot::plot_model(type ="pred",terms =c("age", "smoking"),show.data =TRUE ) +facet_wrap(~group_col, ncol =1) +expand_limits(y =0) +theme(legend.position ="bottom")hers_plot1```No intercept::::::{#fig-hers-with-intercept}```{r}library(sjPlot)hers_plot2 <- hers_lm_with_int |> sjPlot::plot_model(type ="pred",terms =c("age", "smoking"),show.data =TRUE ) +facet_wrap(~group_col, ncol =1) +expand_limits(y =0) +theme(legend.position ="bottom")hers_plot2```With intercept:::`hers` data models with and without intercepts:::### Residuals::: notesMaybe we can transform the data and model in some way to make it easier to inspect.:::{{< include _def-residual-deviation.qmd >}}---:::{#thm-gaussian-resid-noise}#### Residuals in Gaussian modelsIf $Y$ has a Gaussian distribution, then $\err(Y)$ also has a Gaussian distribution, and vice versa.::::::{.proof}Left to the reader.:::---:::{#def-resid-fitted}#### Residuals of a fitted model valueThe **residual of a fitted value $\hat y$** (shorthand: "residual") is its [error](estimation.qmd#def-error) relative to the observed data:$$\bae(\hat y) &\eqdef \erf{\hat y}\\&= y - \hat y\ea$$:::---:::{#exm-resid-bw}#### residuals in `birthweight` data:::{#fig-bw-resids1}```{r}plot1_interact +facet_wrap(~sex) +geom_segment(aes(x = age,y = predlm2,xend = age,yend = weight,col = sex,group = id ),linetype ="dotted" )```Fitted values and residuals for interaction model for `birthweight` data::::::---#### Residuals of fitted values vs residual noise$e(\hat y)$ can be seen as the maximum likelihood estimate of the residual noise:$$\bae(\hy) &= y - \hat y\\ &= \hat\eps_{ML}\ea$$---#### General characteristics of residuals:::{#thm-resid-unbiased}If $\hExpf{Y}$ is an [unbiased](estimation.qmd#sec-unbiased-estimators)estimator of the mean $\Expf{Y}$, then:$$\E{e(y)} = 0$$ {#eq-mean-resid-unbiased}$$\Var{e(y)} \approx \ss$$ {#eq-var-resid-unbiased}:::---:::{.proof}\ @eq-mean-resid-unbiased:$$\ba\Ef{e(y)} &= \Ef{y - \hat y}\\ &= \Ef{y} - \Ef{\hat y}\\ &= \Ef{y} - \Ef{y}\\ &= 0\ea$$@eq-var-resid-unbiased:$$\ba\Var{e(y)} &= \Var{y - \hy}\\ &= \Var{y} + \Var{\hy} - 2 \Cov{y, \hy}\\ &{\dot{\approx}} \Var{y} + 0 - 2 \cdot 0\\ &= \Var{y}\\ &= \ss\ea$$:::---#### Characteristics of residuals in Gaussian modelsWith enough data and a correct model, the residuals will be approximately Guassian distributed, with variance $\sigma^2$, which we can estimate using $\hat\sigma^2$;that is:$$e_i \siid N(0, \hat\sigma^2)$$---#### Computing residuals in RR provides a function for residuals:```{r}resid(bw_lm2)```---:::{#exr-calc-resids}Check R's output by computing the residuals directly.::::::{.solution}\ ```{r}bw$weight -fitted(bw_lm2)```This matches R's output!:::---#### Graphing the residuals:::{#fig-resid-bw layout-ncol=2}:::{#fig-bw-resids1-c2}```{r}plot1_interact +facet_wrap(~sex) +geom_segment(aes(x = age,y = predlm2,xend = age,yend = weight,col = sex,group = id ),linetype ="dotted" )```fitted values::::::{#fig-resids-intxn-bw}```{r}bw <- bw |>mutate(resids_intxn = weight -fitted(bw_lm2) )plot_bw_resid <- bw |>ggplot(aes(x = age,y = resids_intxn,linetype = sex,shape = sex,col = sex )) +theme_bw() +xlab("Gestational age (weeks)") +ylab("residuals (grams)") +theme(legend.position ="bottom") +geom_hline(aes(yintercept =0,col = sex )) +geom_segment(aes(yend =0),linetype ="dotted" ) +geom_point()# expand_limits(y = 0, x = 0) +geom_point(alpha = .7)print(plot_bw_resid +facet_wrap(~sex))```Residuals:::Fitted values and residuals for interaction model for `birthweight` data:::---#### 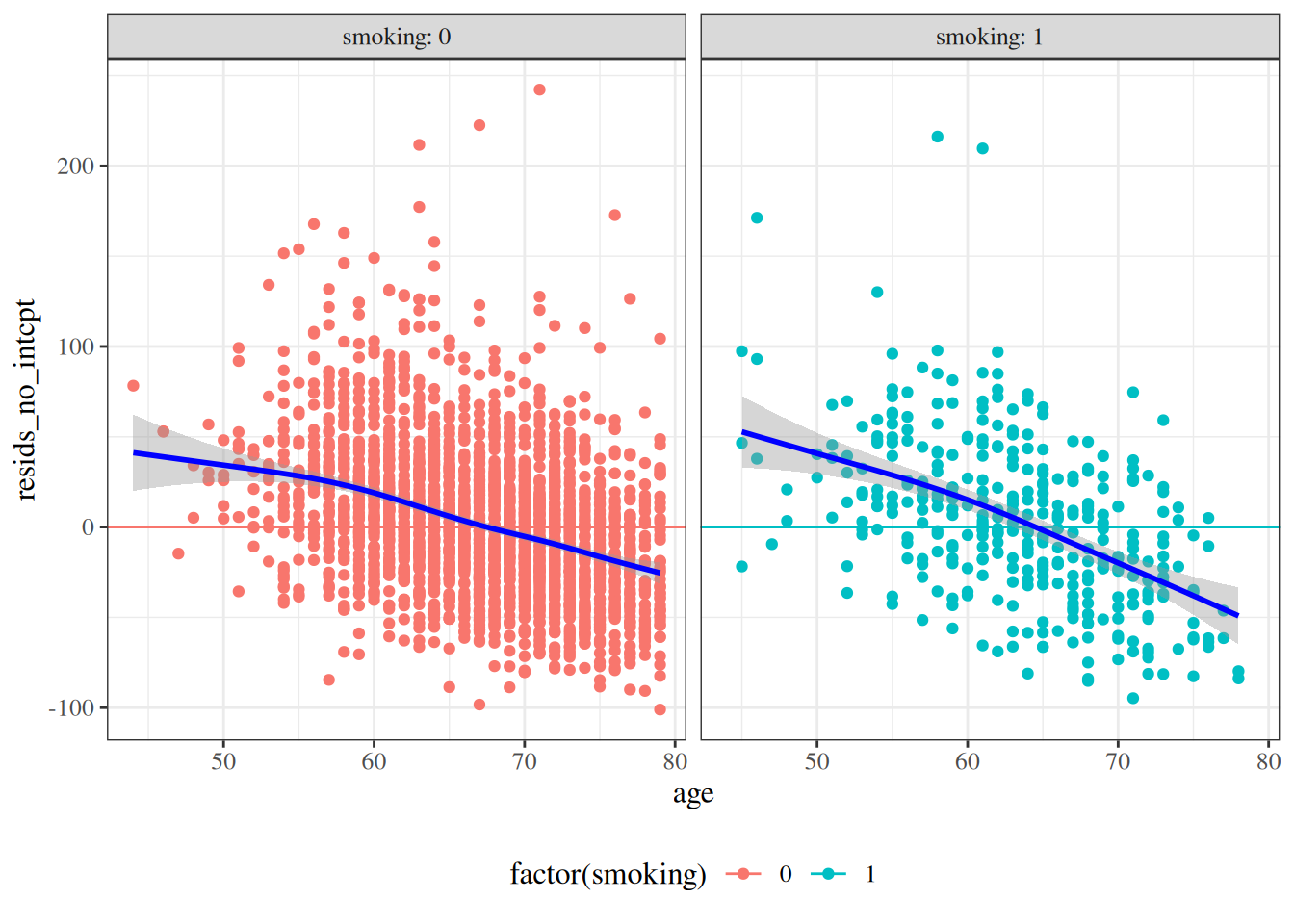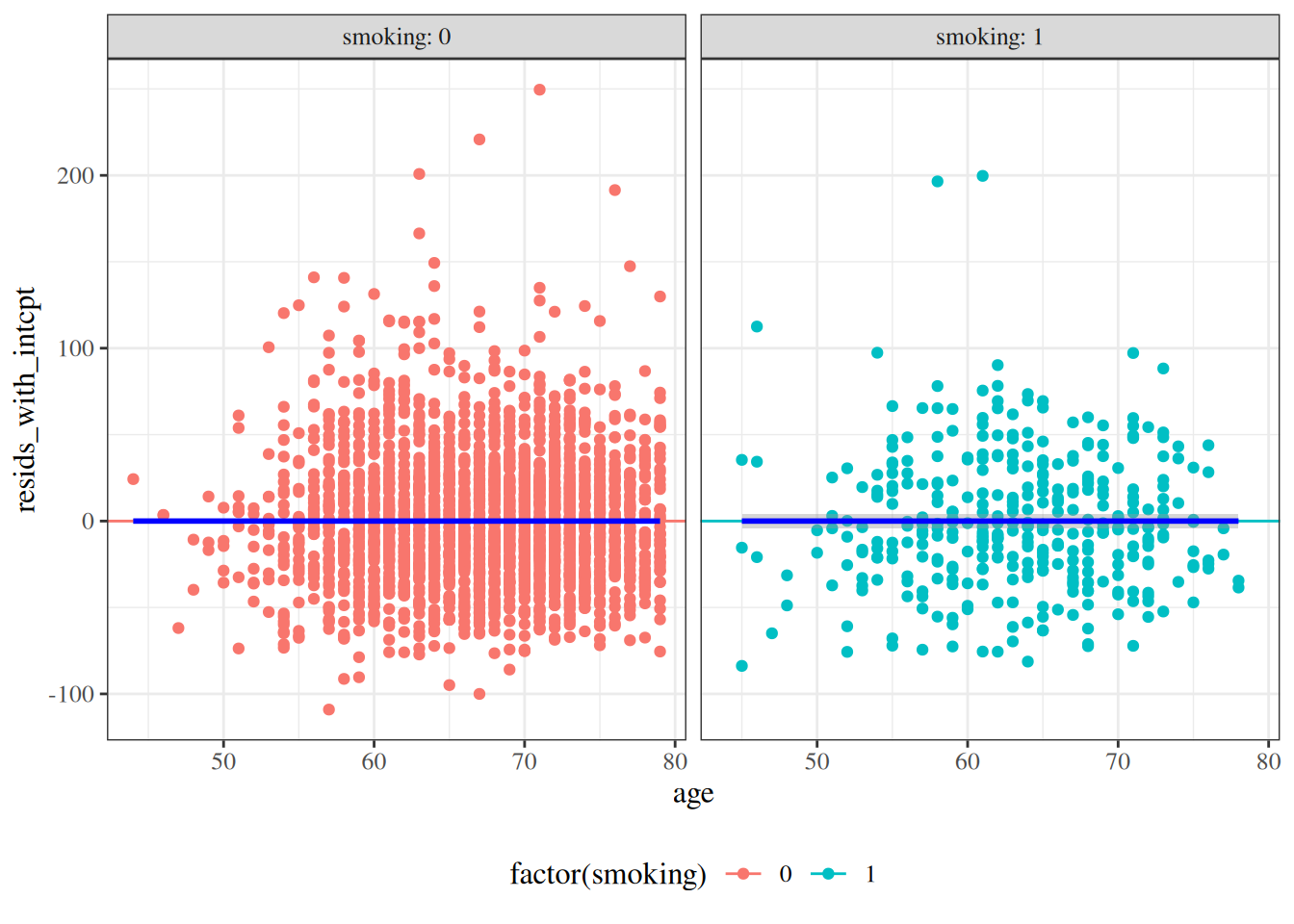Residuals versus predictors```{r}hers <- hers |>mutate(resids_no_intcpt = LDL -fitted(hers_lm_no_int),resids_with_intcpt = LDL -fitted(hers_lm_with_int) )```:::{#fig-resids-hers-1 layout-ncol=2}:::{#fig-resid-hers-pred-no-intcpt} ```{r}hers |>arrange(age) |>ggplot() +aes(x = age, y = resids_no_intcpt, col =factor(smoking)) +geom_point() +geom_hline(aes(yintercept =0, col =factor(smoking))) +facet_wrap(~smoking, labeller ="label_both") +theme(legend.position ="bottom") +geom_smooth(col ="blue")```no intercept::::::{#fig-resid-hers-pred-no-intcpt}```{r}hers |>arrange(age) |>ggplot() +aes(x = age, y = resids_with_intcpt, col =factor(smoking)) +geom_point() +geom_hline(aes(yintercept =0, col =factor(smoking))) +facet_wrap(~smoking, labeller ="label_both") +theme(legend.position ="bottom") +geom_smooth(col ="blue")```with intercept:::Residuals of `hers` data vs predictors:::---#### Residuals versus fitted values::: notesIf the model contains multiple continuous covariates,how do we check for errors in the mean structure assumption?:::```{r}#| label: fig-resids-intxn-hers#| fig-cap: "Residuals of interaction model for `hers` data"library(ggfortify)hers_lm_no_int |>update(na.action = na.omit) |>autoplot(which =1,ncol =1,smooth.colour =NA ) +geom_hline(yintercept =0, col ="red")```---We can add a LOESS smooth to visualize where the residual mean is nonzero:```{r}#| label: fig-resids-intxn-hers-smooth-no-int#| fig-cap: "Residuals of interaction model for `hers` data, no intercept term"library(ggfortify)hers_lm_no_int |>update(na.action = na.omit) |>autoplot(which =1,ncol =1 ) +geom_hline(yintercept =0, col ="red")```---:::{#fig-resid-hers-compare layout-ncol=2}:::{#fig-resids-intxn-hers-smooth-no-int-2}```{r}library(ggfortify)hers_lm_no_int |>update(na.action = na.omit) |>autoplot(which =1,ncol =1 ) +geom_hline(yintercept =0, col ="red")```no intercept term::::::{#fig-resids-intxn-hers-smooth-with-int}```{r}hers_lm_with_int |>update(na.action = na.omit) |>autoplot(which =1,ncol =1 ) +geom_hline(yintercept =0, col ="red")```with intercept term:::Residuals of interaction model for `hers` data, with and without intercept term:::---:::{#def-stred}#### Standardized residuals$$r_i = \frac{e_i}{\widehat{SD}(e_i)}$$:::Hence, with enough data and a correct model, the standardized residuals will be approximately standard Gaussian; that is,$$r_i \siid N(0,1)$$### Marginal distributions of residualsTo look for problems with our model, we can check whether the residuals $e_i$ and standardized residuals $r_i$ look like they have the distributions that they are supposed to have, according to the model.---#### 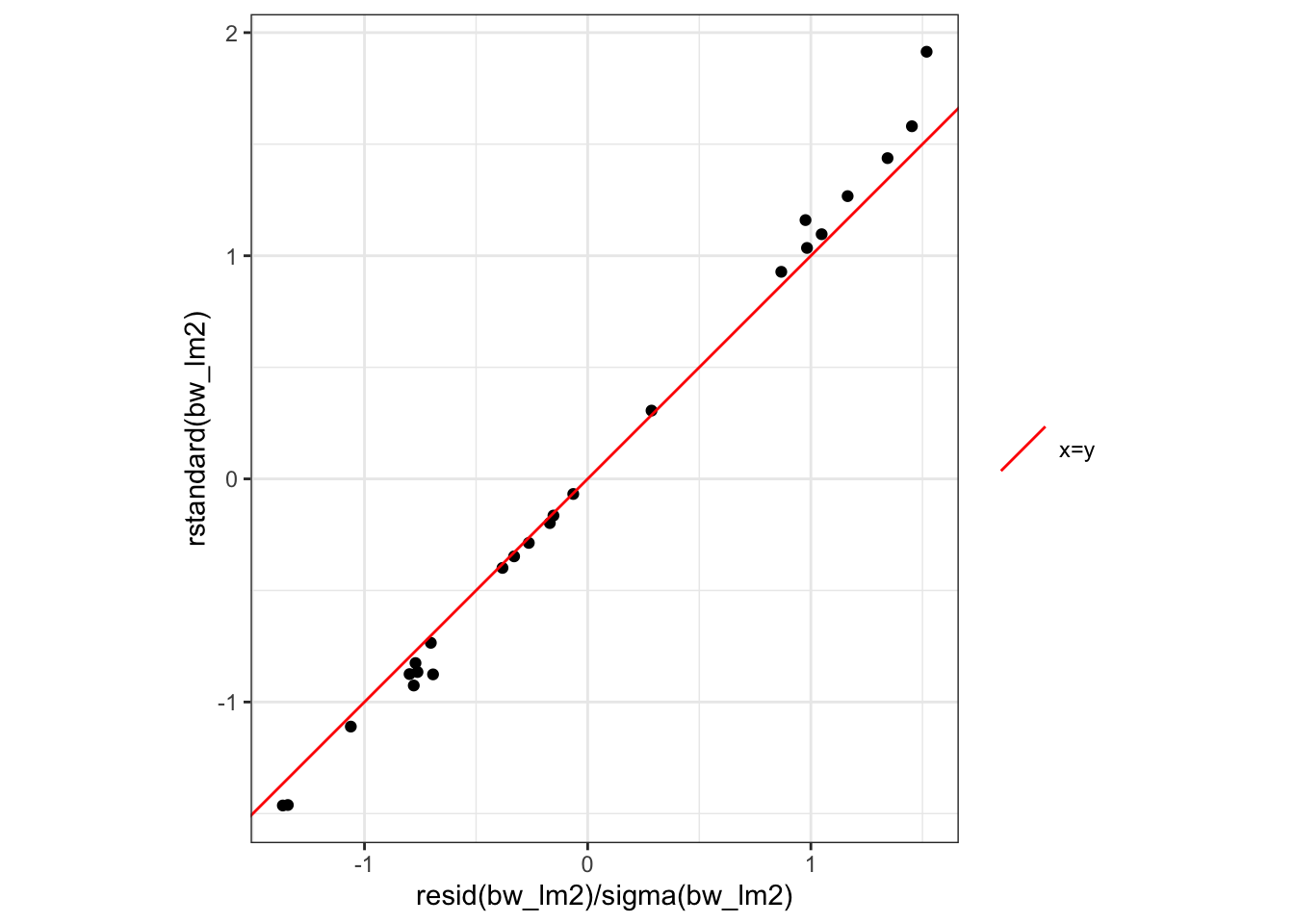Standardized residuals in R```{r}rstandard(bw_lm2)resid(bw_lm2) /sigma(bw_lm2)```::: notesThese are not quite the same, because R is doing something more complicated and precise to get the standard errors. Let's not worry about those details for now; the difference is pretty small in this case::::---```{r}rstandard_compare_plot <-tibble(x =resid(bw_lm2) /sigma(bw_lm2),y =rstandard(bw_lm2) ) |>ggplot(aes(x = x, y = y)) +geom_point() +theme_bw() +coord_equal() +xlab("resid(bw_lm2)/sigma(bw_lm2)") +ylab("rstandard(bw_lm2)") +geom_abline(aes(intercept =0,slope =1,col ="x=y" ) ) +labs(colour ="") +scale_colour_manual(values ="red")print(rstandard_compare_plot)```---Let's add these residuals to the `tibble` of our dataset:```{r}bw <- bw |>mutate(fitted_lm2 =fitted(bw_lm2),resid_lm2 =resid(bw_lm2),resid_lm2_alt = weight - fitted_lm2,std_resid_lm2 =rstandard(bw_lm2),std_resid_lm2_alt = resid_lm2 /sigma(bw_lm2) )bw |>select( sex, age, weight, fitted_lm2, resid_lm2, std_resid_lm2 )```---::: 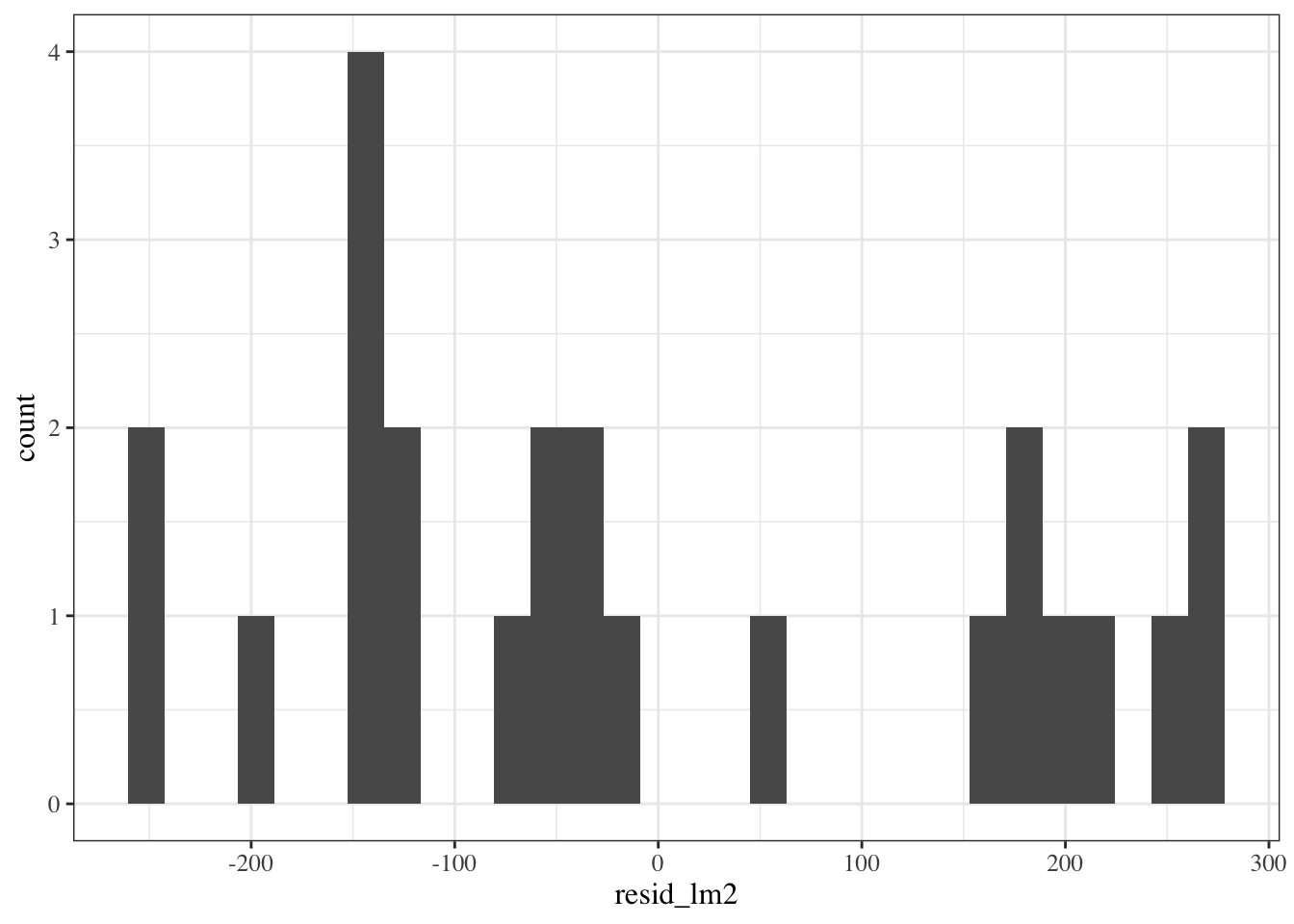notesNow let's build histograms::::```{r}#| fig-cap: "Marginal distribution of (nonstandardized) residuals"#| label: fig-marg-dist-residresid_marginal_hist <- bw |>ggplot(aes(x = resid_lm2)) +geom_histogram()print(resid_marginal_hist)```::: notesHard to tell with this small amount of data, but I'm a bit concerned that the histogram doesn't show a bell-curve shape.:::---```{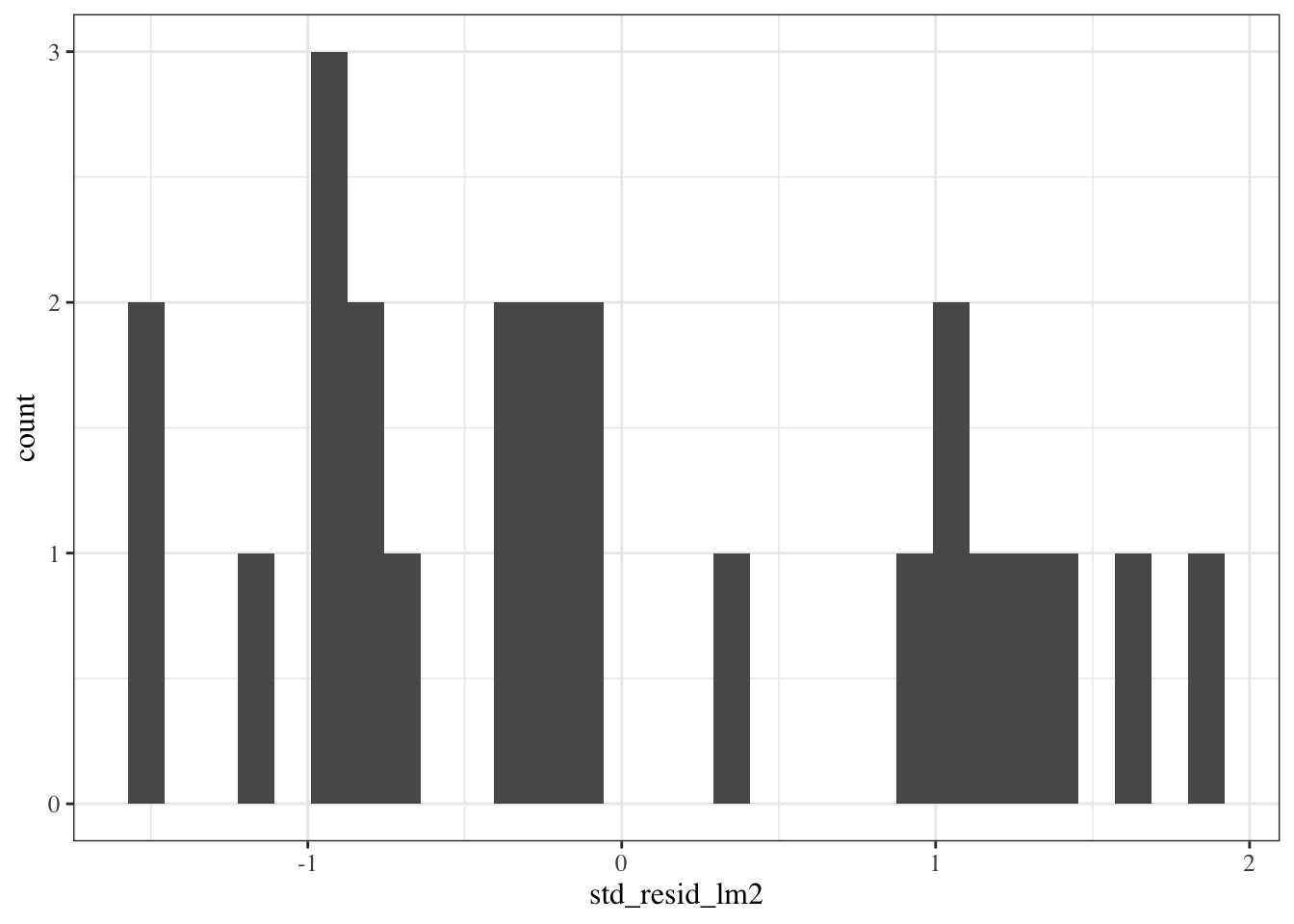r}#| fig-cap: "Marginal distribution of standardized residuals"#| label: fig-marg-stresdstd_resid_marginal_hist <- bw |>ggplot(aes(x = std_resid_lm2)) +geom_histogram()print(std_resid_marginal_hist)```::: notesThis looks similar, although the scale of the x-axis got narrower, because we divided by $\hat\sigma$ (roughly speaking).Still hard to tell if the distribution is Gaussian.:::---### 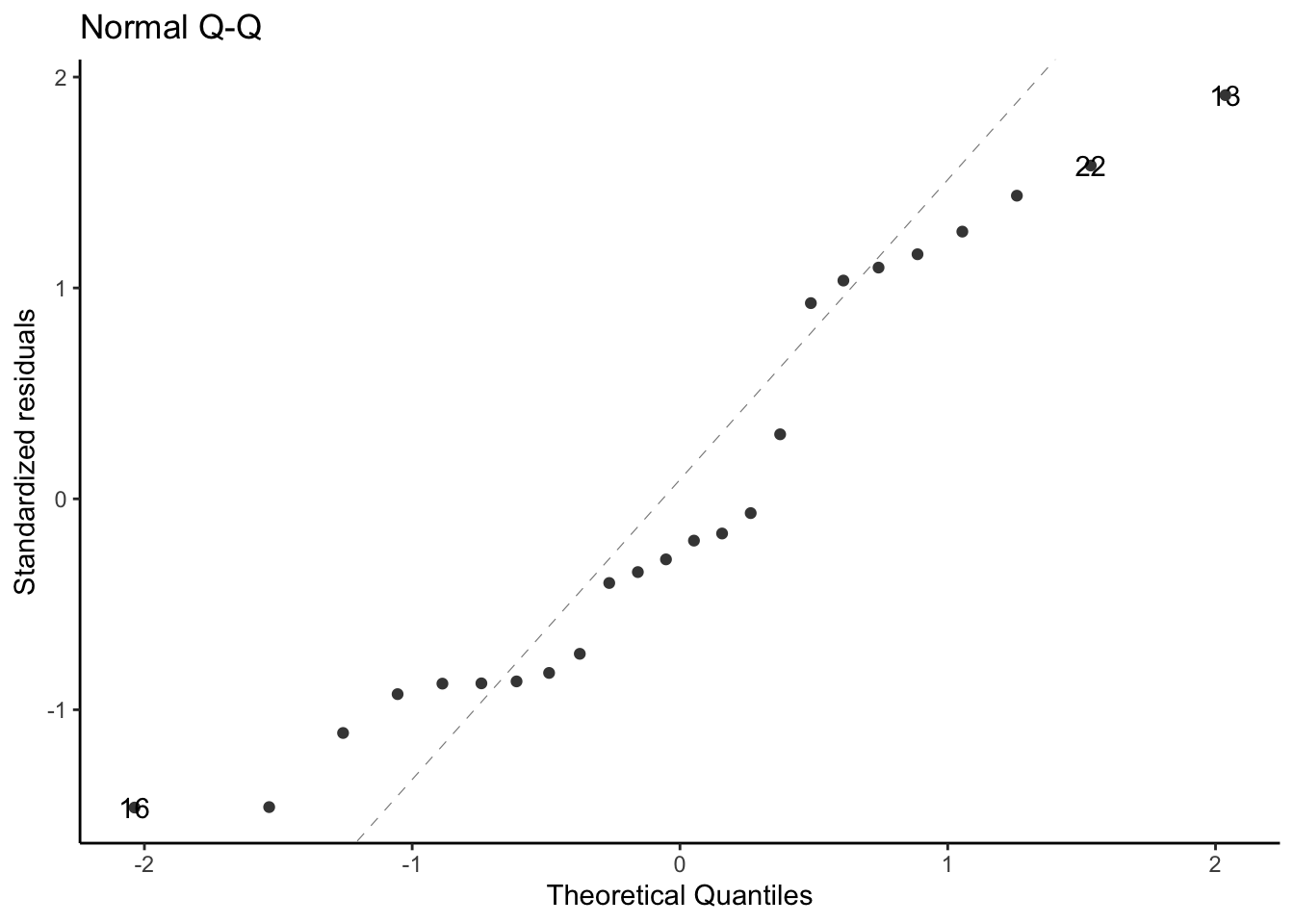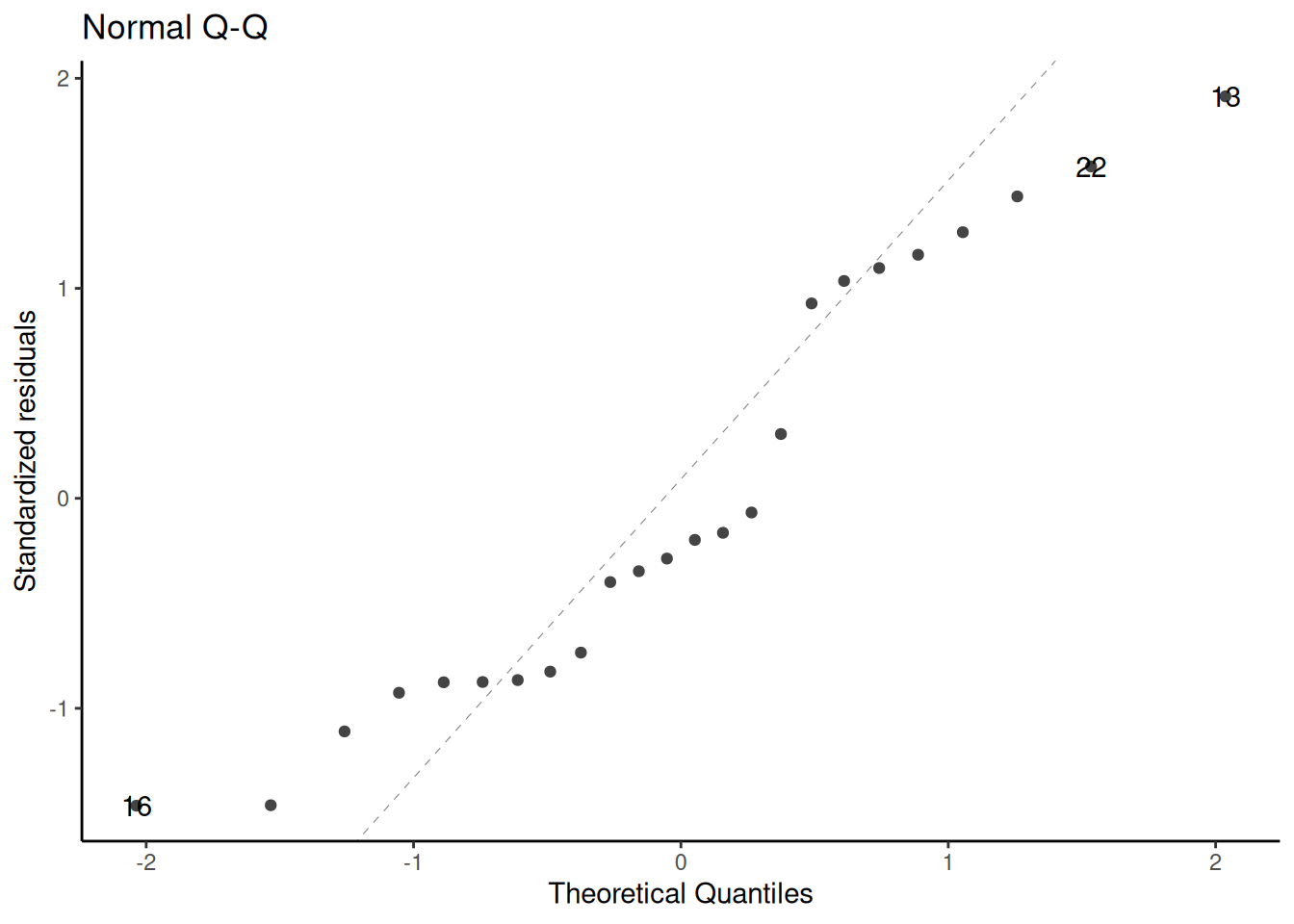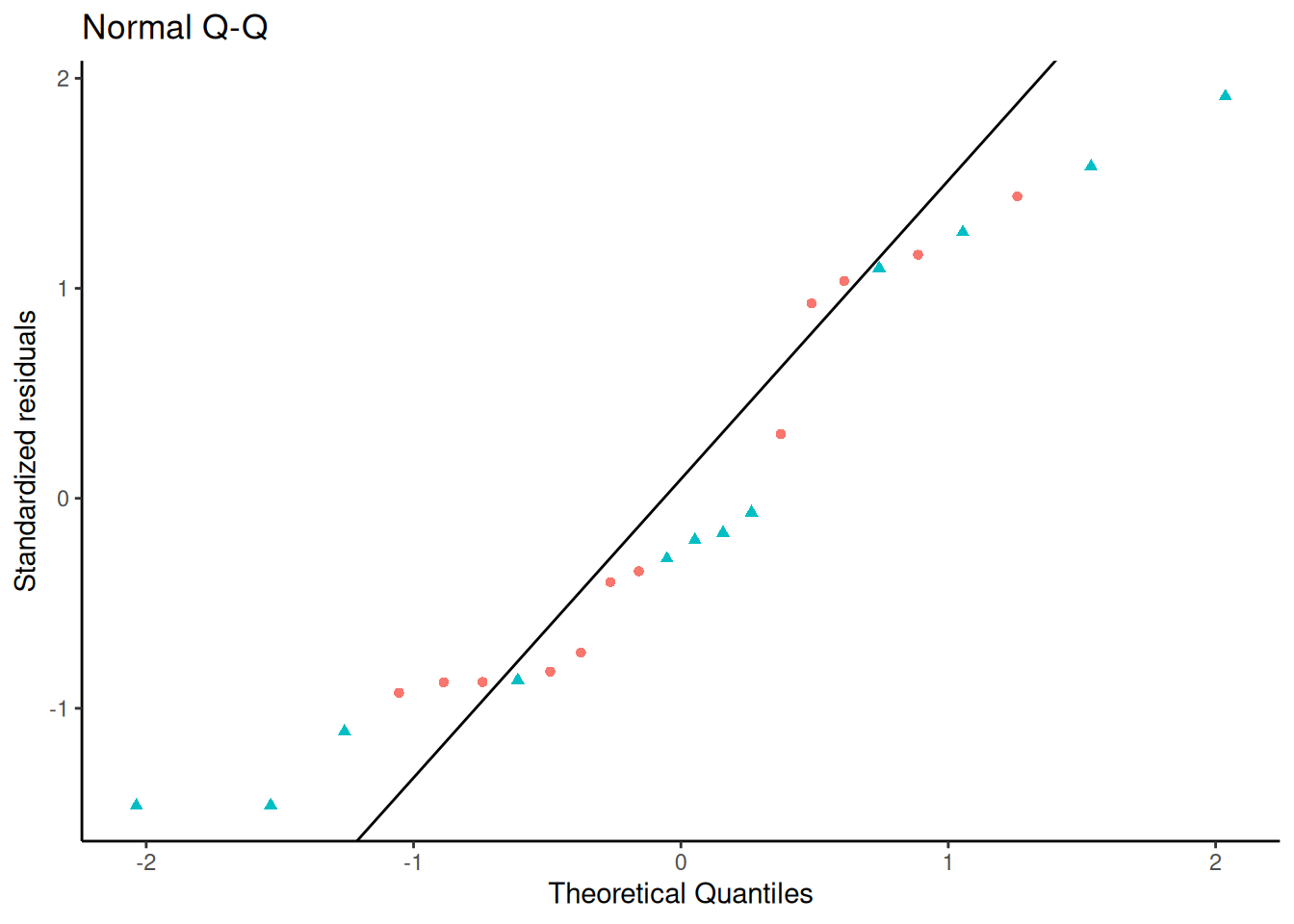QQ plot of standardized residuals::: notesAnother way to assess normality is the QQ plot of the standardized residuals versus normal quantiles::::```{r}library(ggfortify)# needed to make ggplot2::autoplot() work for `lm` objectsqqplot_lm2_auto <- bw_lm2 |>autoplot(which =2, # options are 1:6; can do multiple at oncencol =1 ) +theme_classic()print(qqplot_lm2_auto)```::: notesIf the Gaussian model were correct, these points should follow the dotted line.Fig 2.4 panel (c) in @dobson4e is a little different; they didn't specify how they produced it, but other statistical analysis systems do things differently from R.See also @dunn2018generalized [§3.5.4](https://link.springer.com/chapter/10.1007/978-1-4419-0118-7_3#Sec14:~:text=3.5.4%20Q%E2%80%93Q%20Plots%20and%20Normality).:::---#### QQ plot - how it's built::: notesLet's construct it by hand::::```{r}bw <- bw |>mutate(p = (rank(std_resid_lm2) -1/2) /n(), # "Blom's method"expected_quantiles_lm2 =qnorm(p) )qqplot_lm2 <- bw |>ggplot(aes(x = expected_quantiles_lm2,y = std_resid_lm2,col = sex,shape = sex ) ) +geom_point() +theme_classic() +theme(legend.position ="none") +# removing the plot legendggtitle("Normal Q-Q") +xlab("Theoretical Quantiles") +ylab("Standardized residuals")# find the expected line:ps <-c(.25, .75) # reference probabilitiesa <-quantile(rstandard(bw_lm2), ps) # empirical quantilesb <-qnorm(ps) # theoretical quantilesqq_slope <-diff(a) /diff(b)qq_intcpt <- a[1] - b[1] * qq_slopeqqplot_lm2 <- qqplot_lm2 +geom_abline(slope = qq_slope, intercept = qq_intcpt)print(qqplot_lm2)```---### Conditional distributions of residualsIf our Gaussian linear regression model is correct, the residuals $e_i$ and standardized residuals $r_i$ should have:- an approximately Gaussian distribution, with:- a mean of 0- a constant varianceThis should be true **for every** value of $x$.---If we didn't correctly guess the functional form of the linear component of the mean, $$\text{E}[Y|X=x] = \beta_0 + \beta_1 X_1 + ... 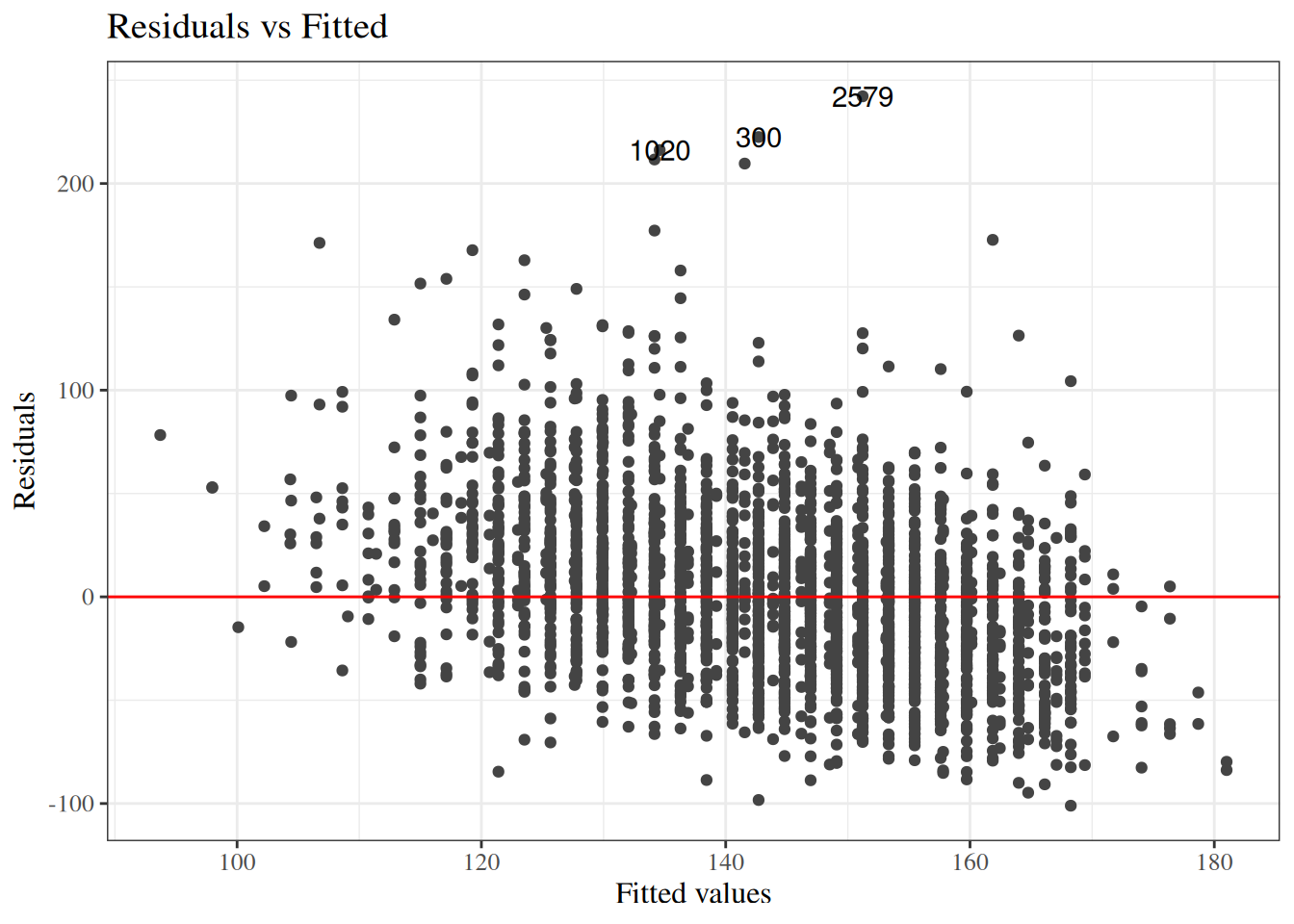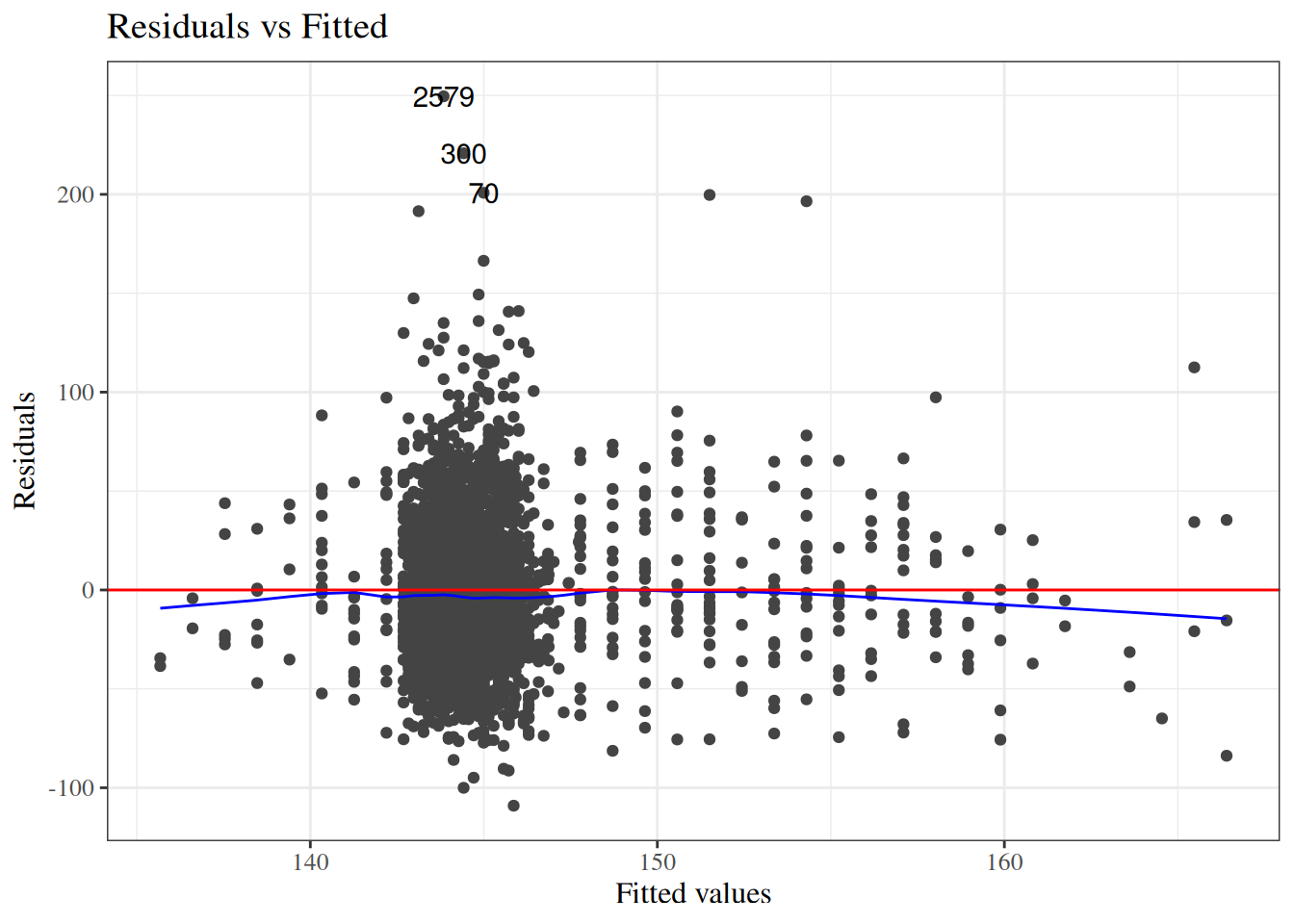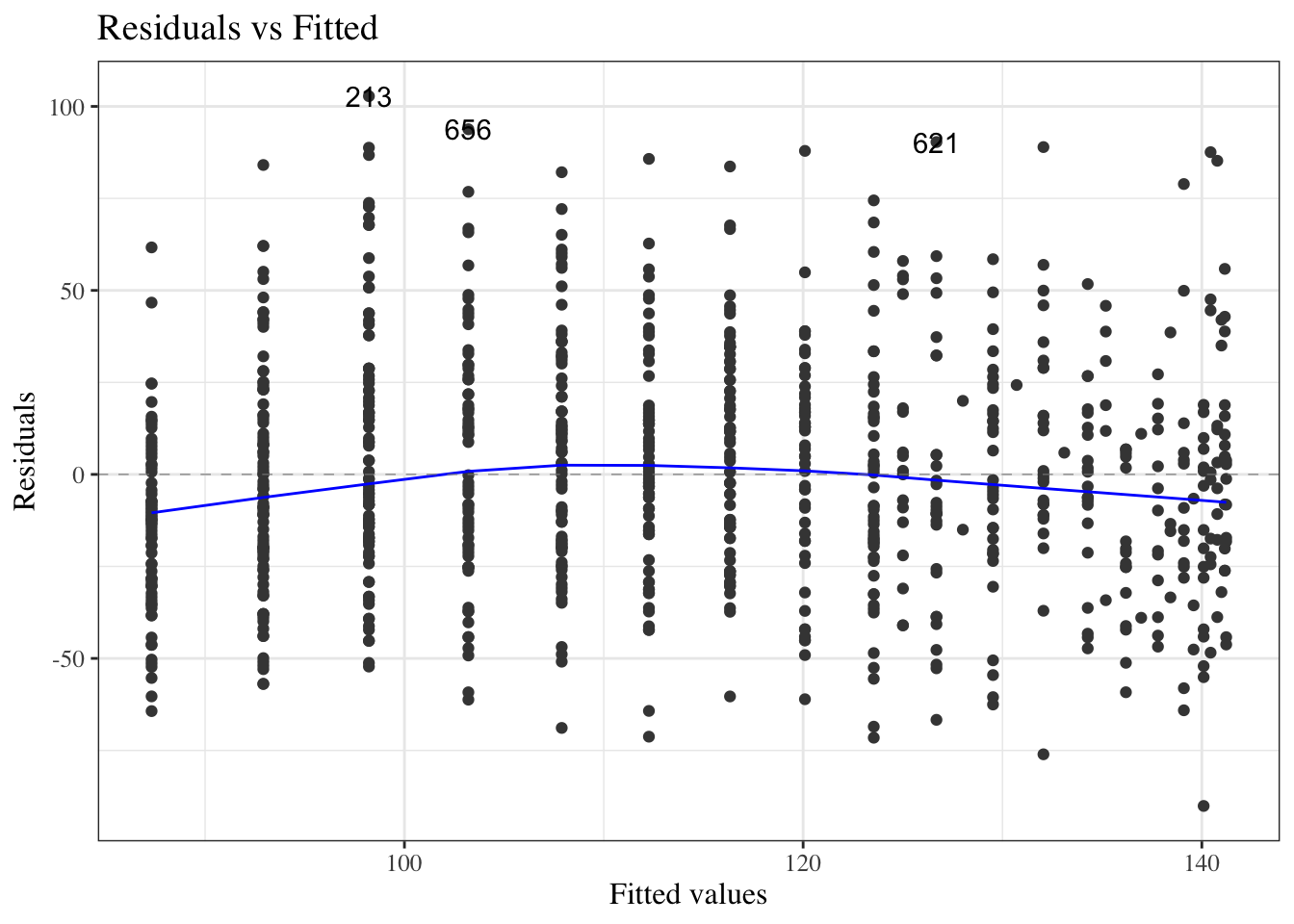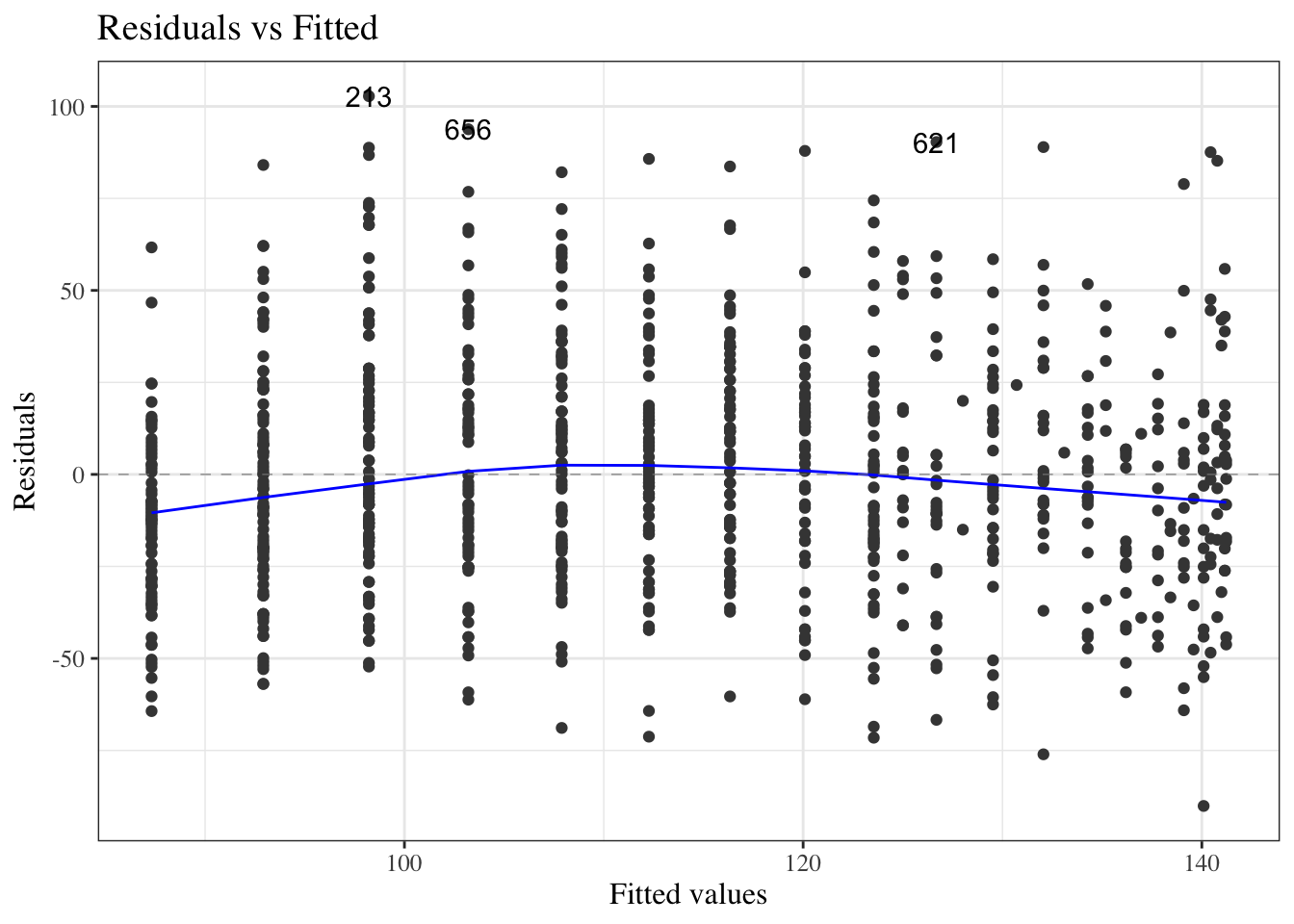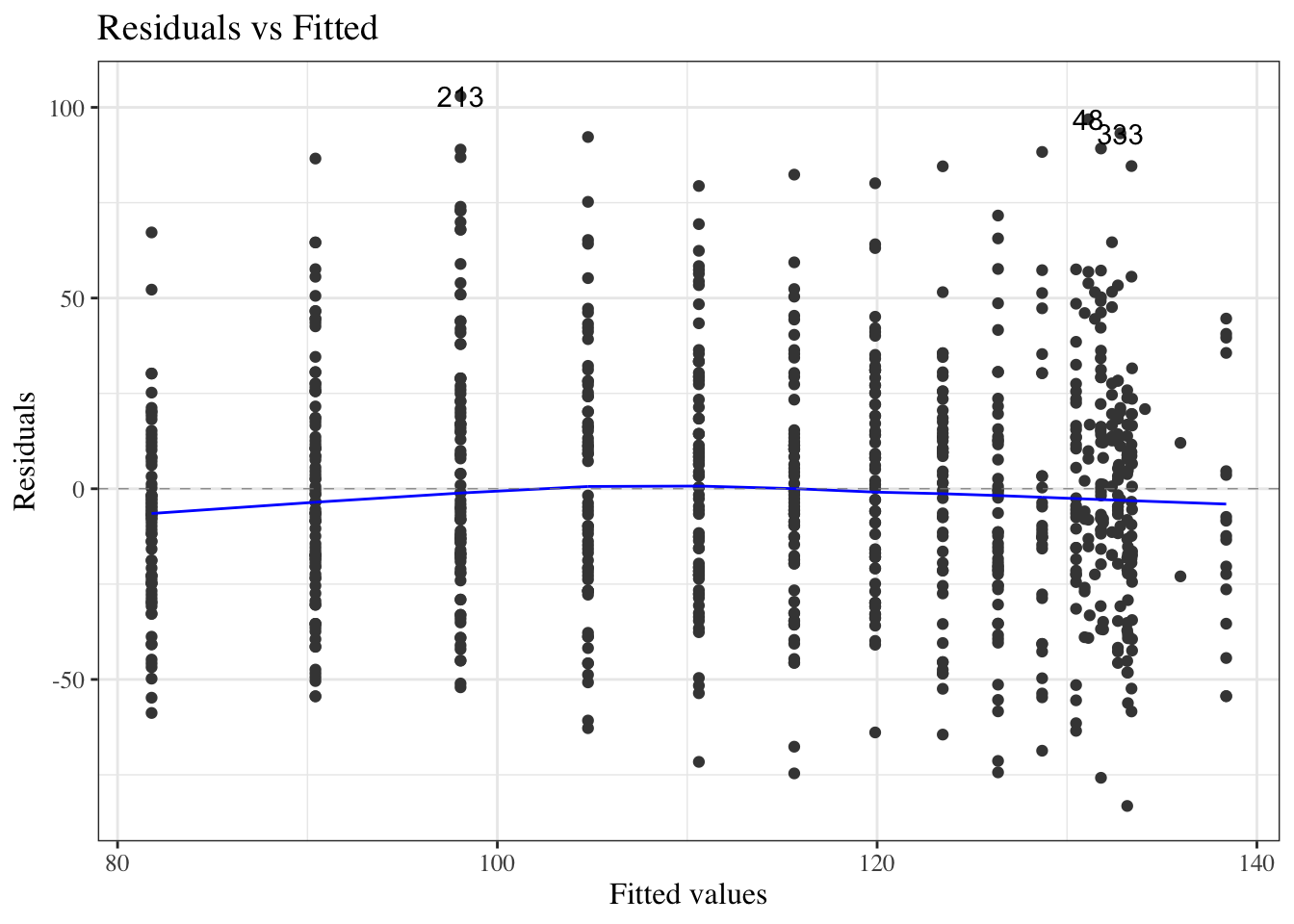+ \beta_p X_p$$Then the residuals might have nonzero mean.Regardless of whether we guessed the mean function correctly, ther the variance of the residuals might differ between values of $x$.---#### Residuals versus fitted values::: notesTo look for these issues, we can plot the residuals $e_i$ against the fitted values $\hat y_i$ (@fig-bw_lm2-resid-vs-fitted).::::::{#fig-bw_lm2-resid-vs-fitted}```{r}autoplot(bw_lm2, which =1, ncol =1) |>print()````birthweight` model (@eq-BW-lm-interact): residuals versus fitted values:::::: notesIf the model is correct, the blue line should stay flat and close to 0, and the cloud of dots should have the same vertical spread regardless of the fitted value.If not, we probably need to change the functional form of linear component of the mean, $$\text{E}[Y|X=x] = \beta_0 + \beta_1 X_1 + ... 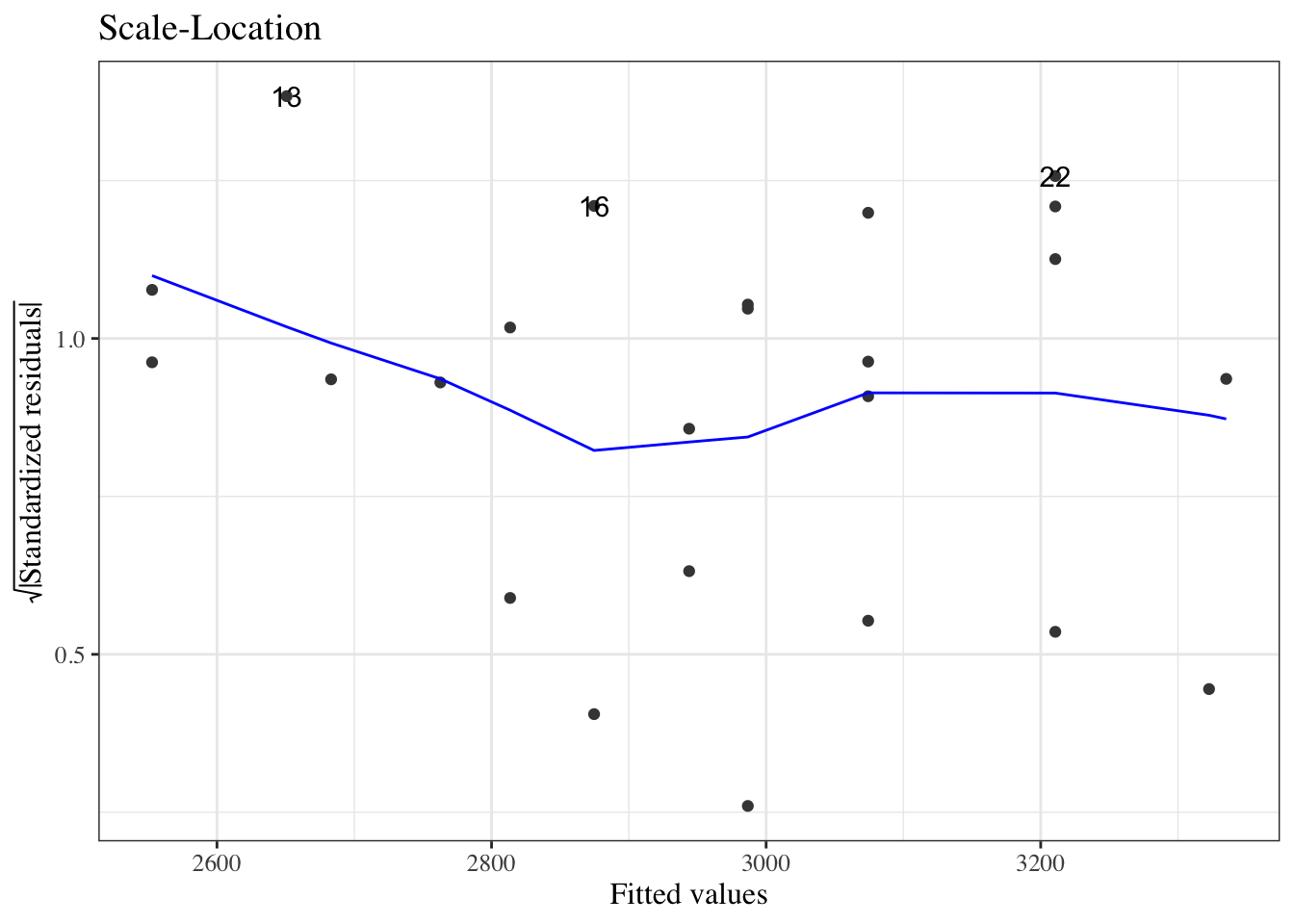+ \beta_p X_p$$:::---{{< include exm-plot-fits.qmd >}}---#### Scale-location plot::: notesWe can also plot the square roots of the absolute values of the standardized residuals against the fitted values (@fig-bw-scale-loc).:::```{r}#| label: fig-bw-scale-loc#| fig-cap: "Scale-location plot of `birthweight` data"autoplot(bw_lm2, which =3, ncol =1) |>print()```::: notesHere, the blue line doesn't need to be near 0, but it should be flat. 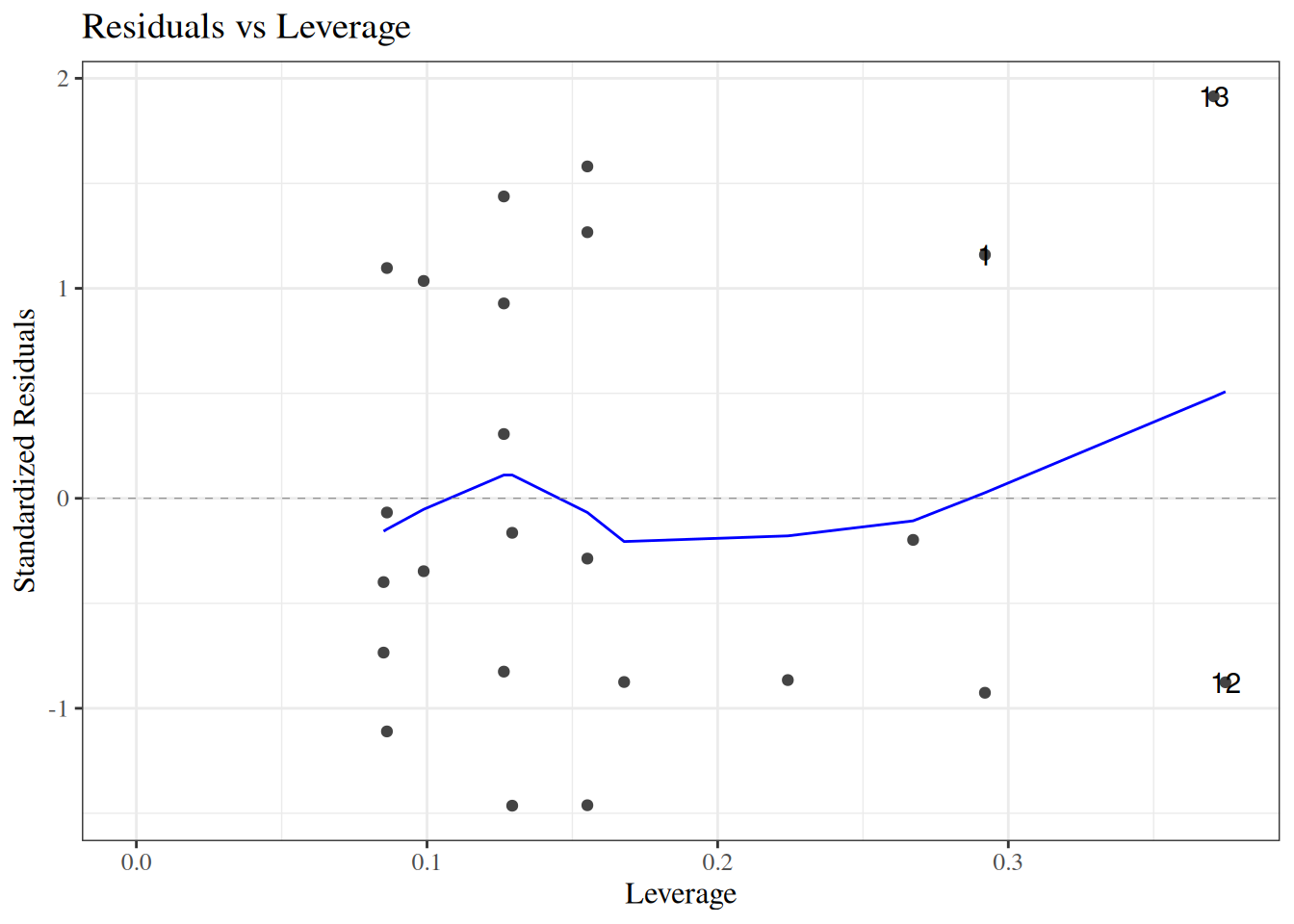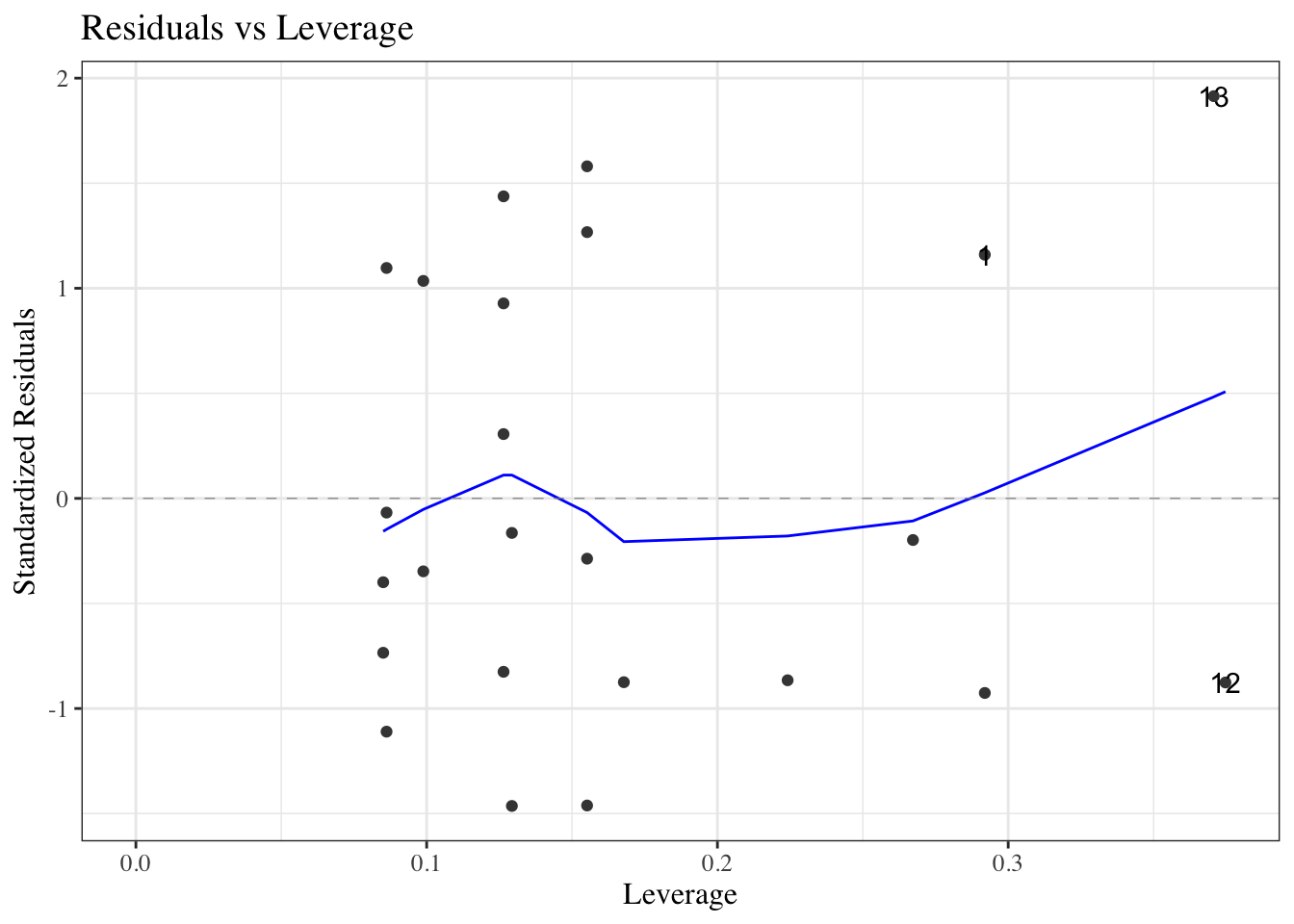If not, the residual variance $\sigma^2$ might not be constant, and we might need to transform our outcome $Y$ (or use a model that allows non-constant variance).:::---#### Residuals versus leverage::: notesWe can also plot our standardized residuals against "leverage", which roughly speaking is a measure of how unusual each $x_i$ value is. Very unusual $x_i$ values can have extreme effects on the model fit, so we might want to remove those observations as outliers, particularly if they have large residuals.:::::: {#fig-bw_lm2_resid-vs-leverage}```{r}autoplot(bw_lm2, which =5, ncol =1) |>print()````birthweight` model with interactions (@eq-BW-lm-interact): residuals versus leverage:::::: notesThe blue line should be relatively flat and close to 0 here.:::---### 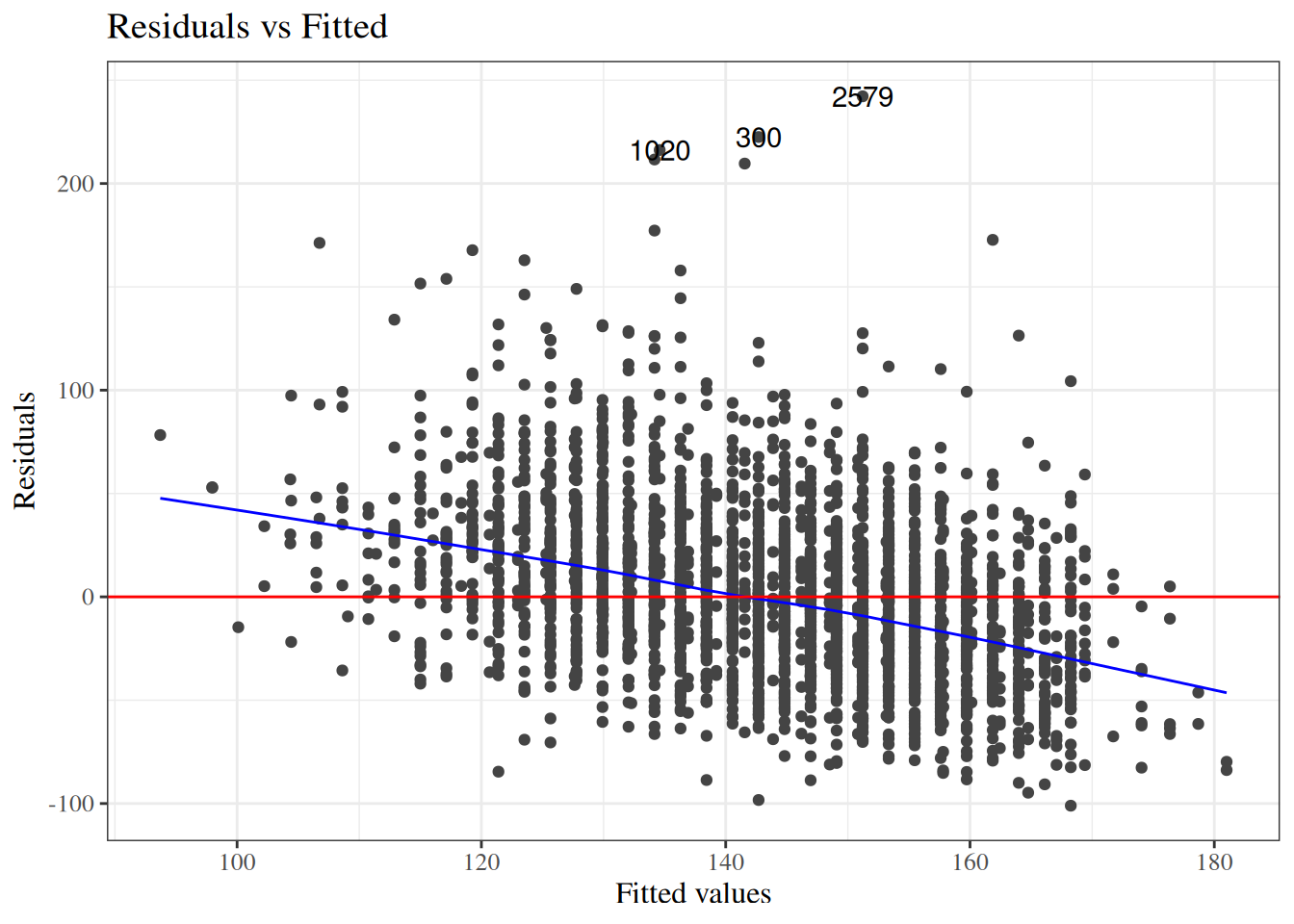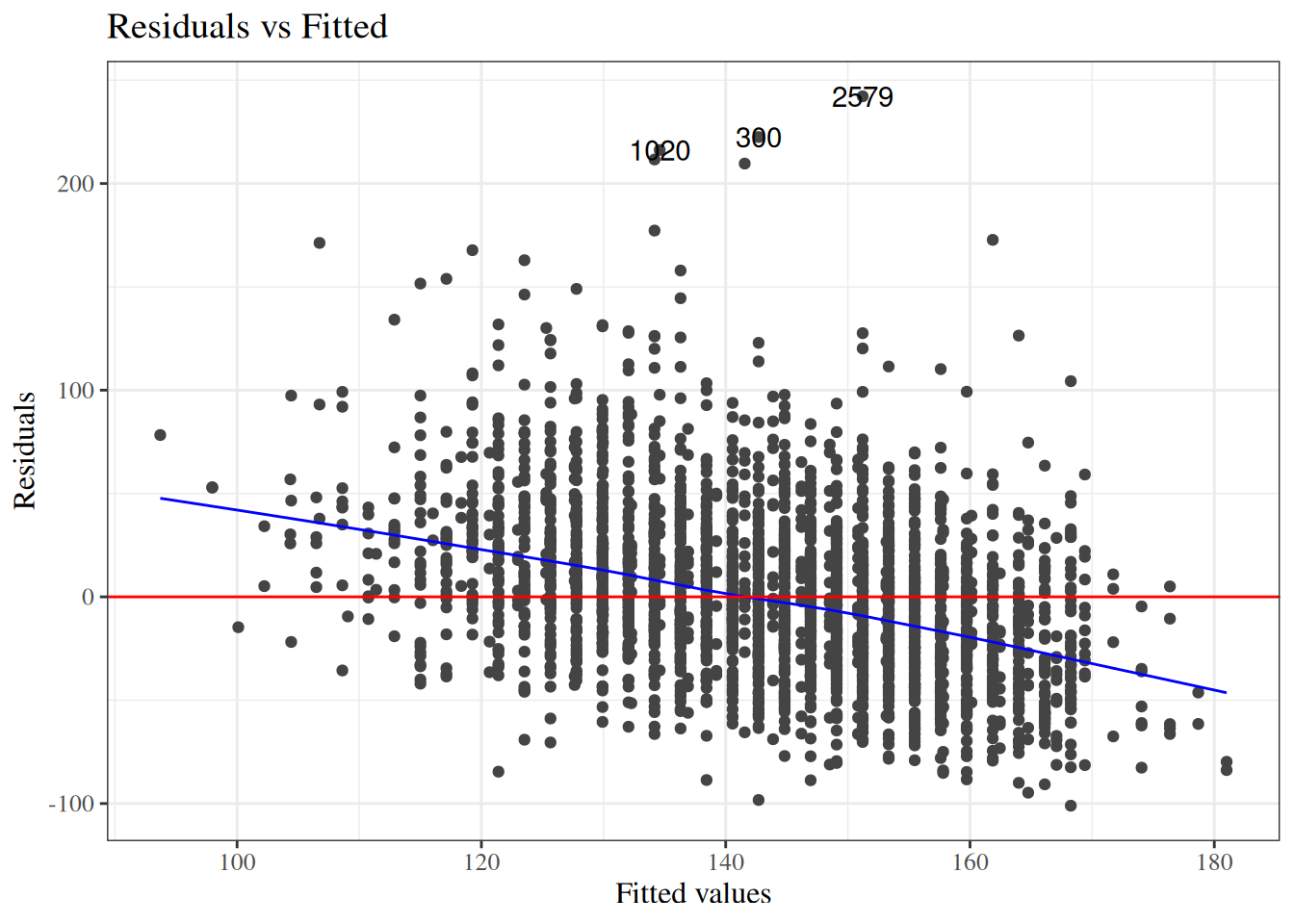Diagnostics constructed by hand```{r}bw <- bw |>mutate(predlm2 =predict(bw_lm2),residlm2 = weight - predlm2,std_resid = residlm2 /sigma(bw_lm2),# std_resid_builtin = rstandard(bw_lm2), # uses leveragesqrt_abs_std_resid = std_resid |>abs() |>sqrt() )```##### Residuals vs fitted```{r}resid_vs_fit <- bw |>ggplot(aes(x = predlm2, y = residlm2, col = sex, shape = sex) ) +geom_point() +theme_classic() +geom_hline(yintercept =0)print(resid_vs_fit)```##### Standardized residuals vs fitted```{r}bw |>ggplot(aes(x = predlm2, y = std_resid, col = sex, shape = sex) ) +geom_point() +theme_classic() +geom_hline(yintercept =0)```##### 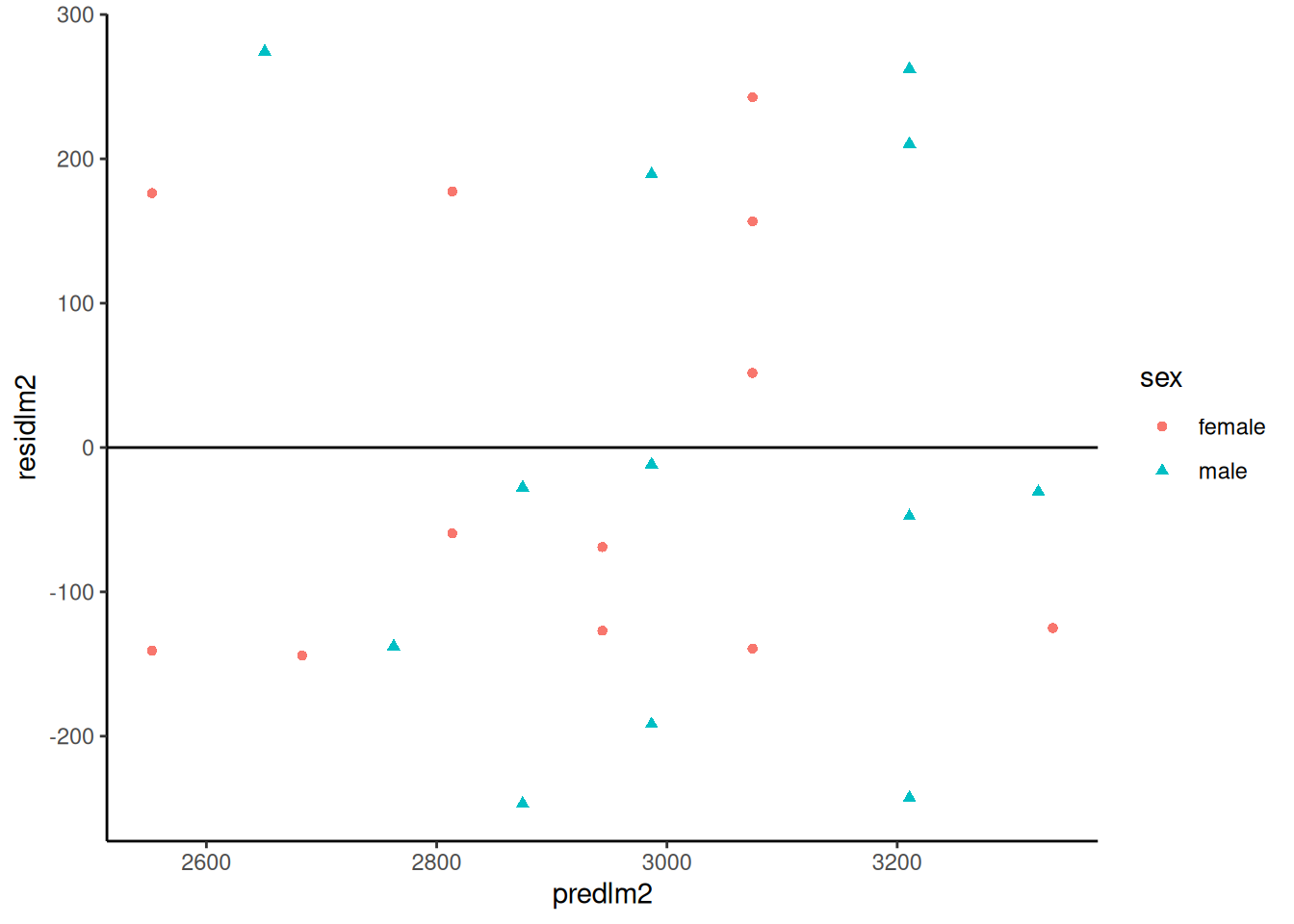Standardized residuals vs gestational age```{r}bw |>ggplot(aes(x = age, y = std_resid, col = sex, shape = sex) ) +geom_point() +theme_classic() +geom_hline(yintercept =0)```##### `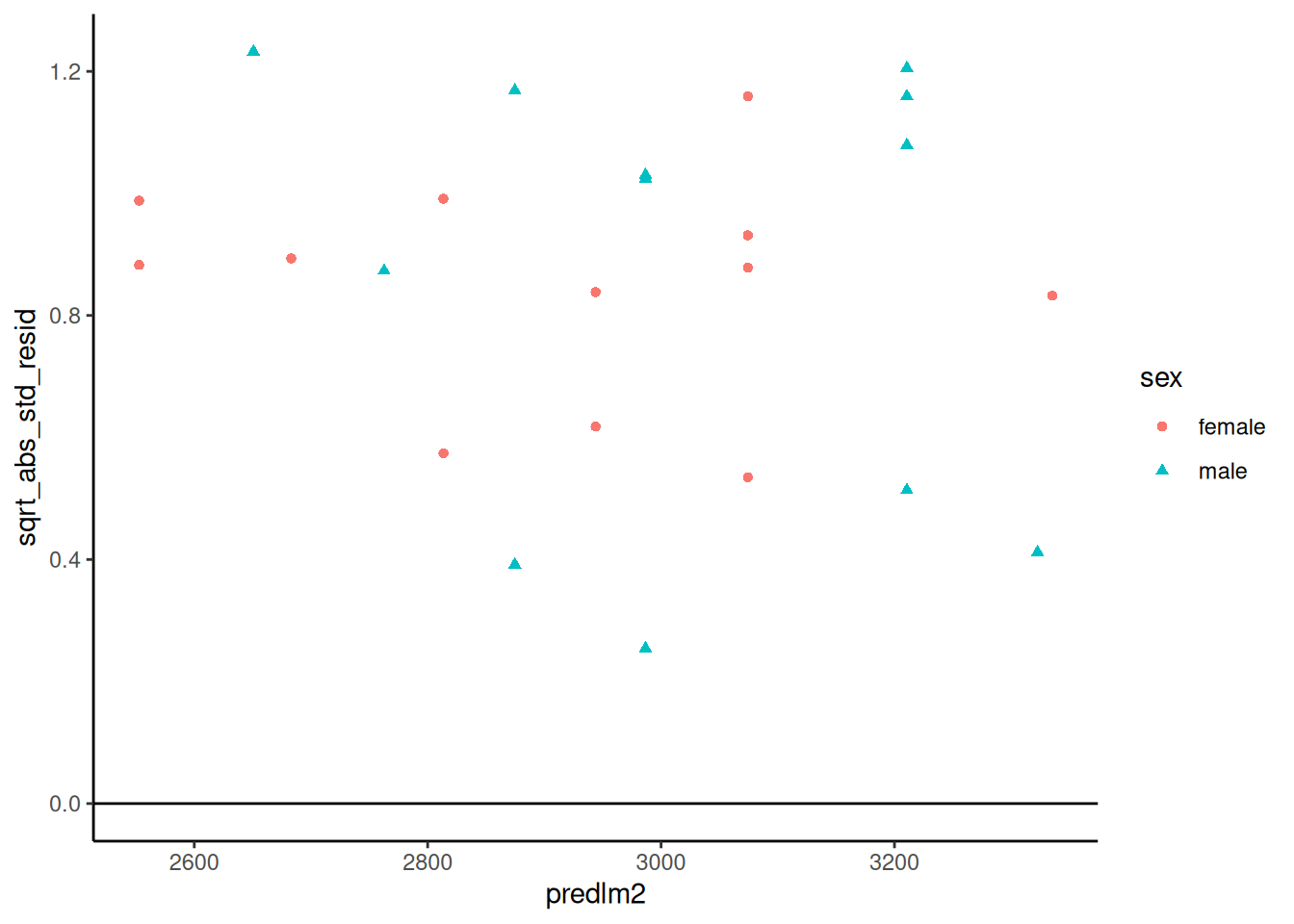sqrt(abs(rstandard()))` vs fittedCompare with `autoplot(bw_lm2, 3)````{r}bw |>ggplot(aes(x = predlm2, y = sqrt_abs_std_resid, col = sex, shape = sex) ) +geom_point() +theme_classic() +geom_hline(yintercept =0)```## Model selection(adapted from @dobson4e §6.3.3; for more information on prediction, see @james2013introduction and @rms2e).::: notesIf we have a lot of covariates in our dataset, we might want to choose a small subset to use in our model.There are a few possible metrics to consider for choosing a "best" model.:::### Mean squared errorWe might want to minimize the **mean squared error**, $\text E[(y-\hat y)^2]$, for new observations that weren't in our data set when we fit the model.Unfortunately, $$\frac{1}{n}\sum_{i=1}^n (y_i-\hat y_i)^2$$ gives a biased estimate of $\text E[(y-\hat y)^2]$ for new data. If we want an unbiased estimate, we will have to be clever.---#### Cross-validation```{r}data("carbohydrate", package ="dobson")library(cvTools)full_model <-lm(carbohydrate ~ ., data = carbohydrate)cv_full <- full_model |>cvFit(data = carbohydrate, K =5, R =10,y = carbohydrate$carbohydrate )reduced_model <- full_model |>update(formula =~ . 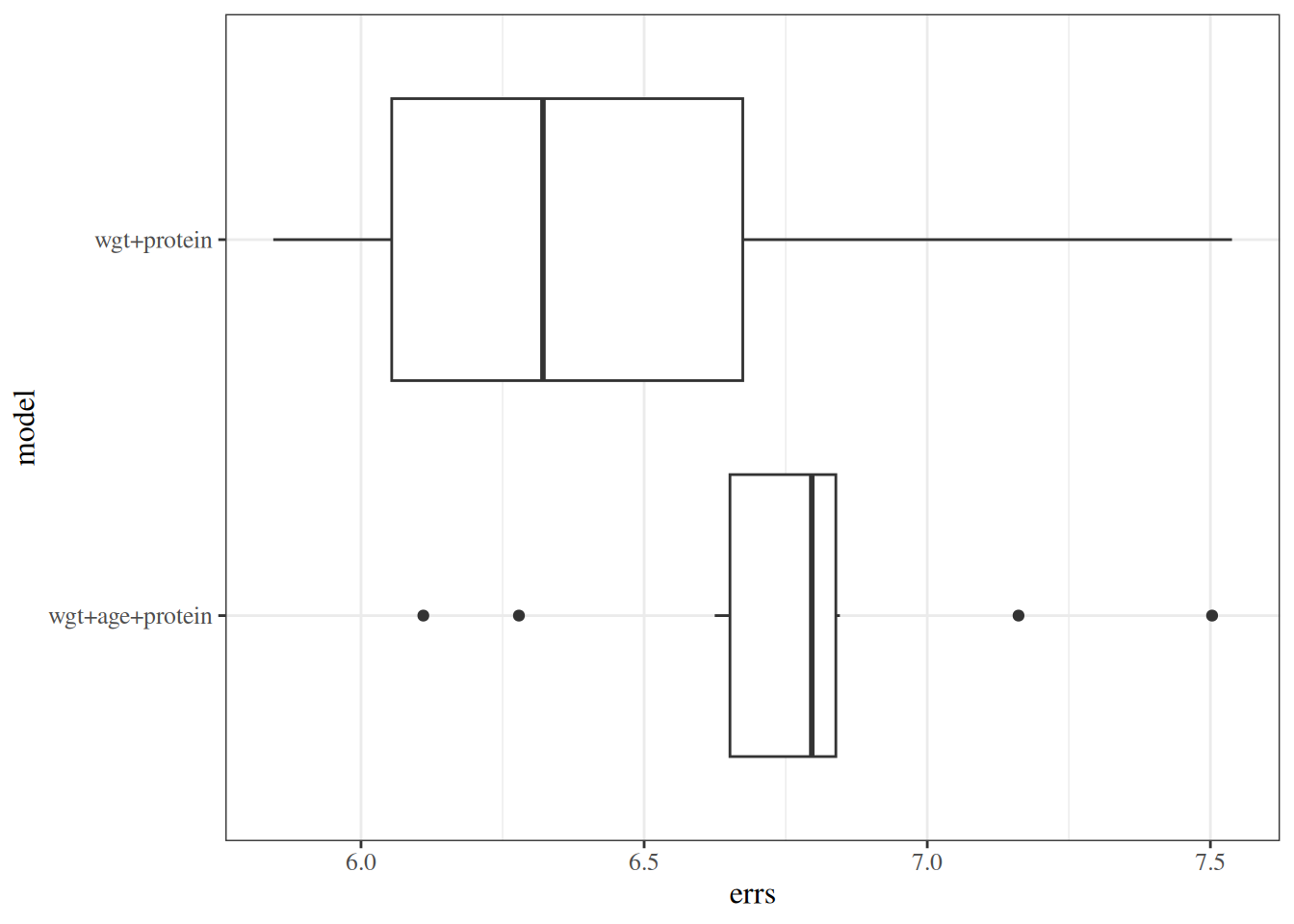- age)cv_reduced <- reduced_model |>cvFit(data = carbohydrate, K =5, R =10,y = carbohydrate$carbohydrate )```---```{r}results_reduced <-tibble(model ="wgt+protein",errs = cv_reduced$reps[] )results_full <-tibble(model ="wgt+age+protein",errs = cv_full$reps[] )cv_results <-bind_rows(results_reduced, results_full)cv_results |>ggplot(aes(y = model, x = errs)) +geom_boxplot()```---##### comparing metrics```{r}compare_results <-tribble(~model, ~cvRMSE, ~r.squared, ~adj.r.squared, ~trainRMSE, ~loglik,"full", cv_full$cv,summary(full_model)$r.squared,summary(full_model)$adj.r.squared,sigma(full_model),logLik(full_model) |>as.numeric(),"reduced", cv_reduced$cv,summary(reduced_model)$r.squared,summary(reduced_model)$adj.r.squared,sigma(reduced_model),logLik(reduced_model) |>as.numeric())compare_results```---```{r}anova(full_model, reduced_model)```---#### stepwise regression```{r}library(olsrr)olsrr:::ols_step_both_aic(full_model)```---#### Lasso$$\am_{\theta} \cb{\llik(\th) - \lambda \sum_{j=1}^p|\beta_j|}$$```{r}library(glmnet)y <- carbohydrate$carbohydratex <- carbohydrate |>select(age, weight, protein) |>as.matrix()fit <-glmnet(x, y)```---```{r}#| fig-cap: "Lasso selection"#| label: fig-carbs-lassoautoplot(fit, xvar ="lambda")```---```{r}cvfit <-cv.glmnet(x, y)plot(cvfit)```---```{r}coef(cvfit, s ="lambda.1se")```## Categorical covariates with more than two levels### Example: `birthweight`In the birthweight example, the variable `sex` had only two observed values:```{r}unique(bw$sex)```If there are more than two observed values, we can't just use a single variable with 0s and 1s.### :::{.notes}For example, @tbl-iris-data shows the [(in)famous](https://www.meganstodel.com/posts/no-to-iris/)`iris` data (@anderson1935irises), and @tbl-iris-summary provides summary statistics. The data include three species: "setosa", "versicolor", and "virginica".:::```{r}#| tbl-cap: "The `iris` data"#| label: tbl-iris-datahead(iris)``````{r}#| tbl-cap: "Summary statistics for the `iris` data"#| label: tbl-iris-summarylibrary(table1)table1(x =~ . 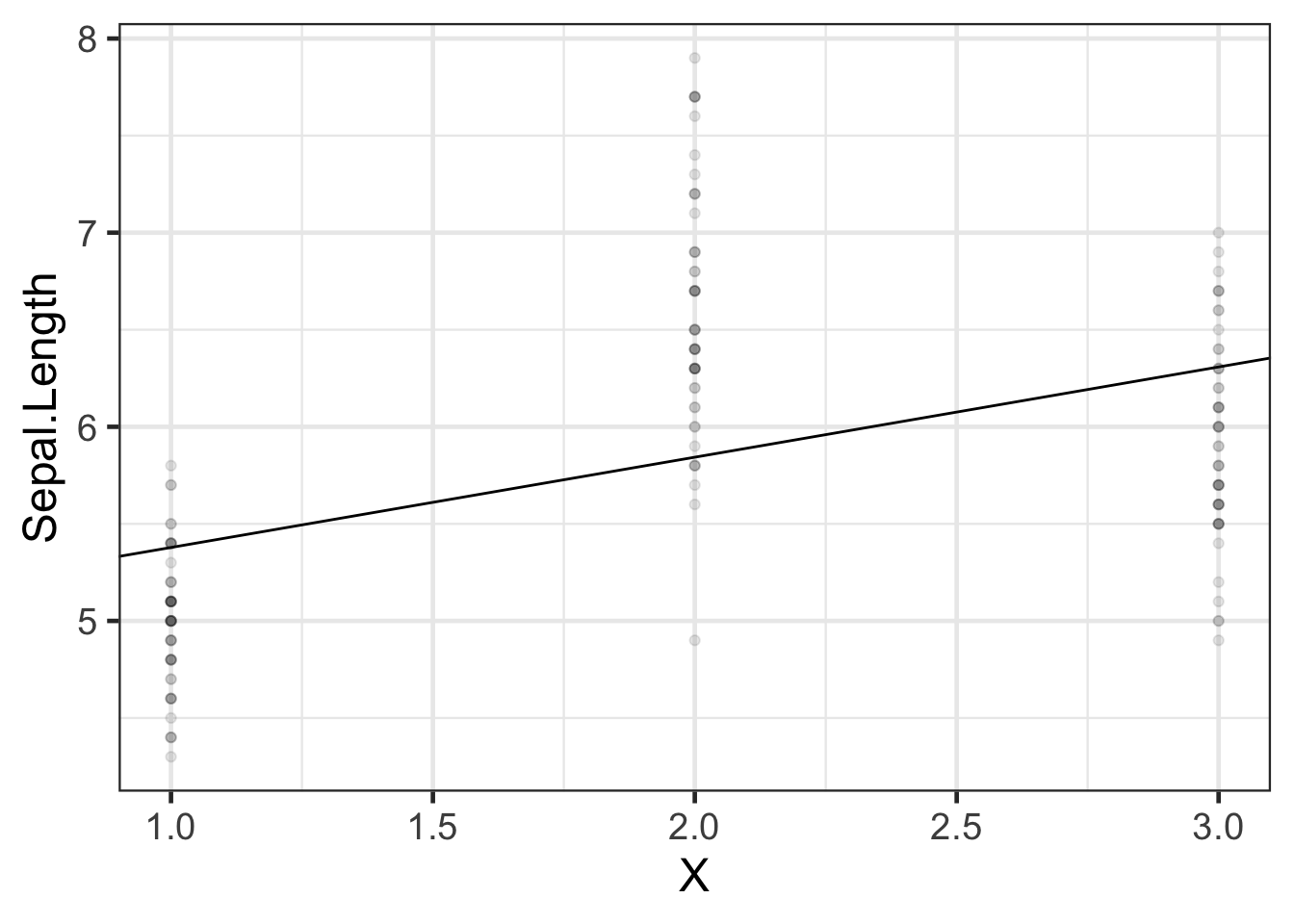| Species,data = iris,overall =FALSE)```---If we want to model `Sepal.Length` by species, we could create a variable $X$ that represents "setosa" as $X=1$, "virginica" as $X=2$, and "versicolor" as $X=3$.```{r}#| label: tbl-numeric-coding#| tbl-cap: "`iris` data with numeric coding of species"data(iris) # this step is not always necessary, but ensures you're starting# from the original version of a dataset stored in a loaded packageiris <- iris |>tibble() |>mutate(X =case_when( Species =="setosa"~1, Species =="virginica"~2, Species =="versicolor"~3 ) )iris |>distinct(Species, X)```Then we could fit a model like:```{r}#| label: tbl-iris-numeric-species#| tbl-cap: "Model of `iris` data with numeric coding of `Species`"iris_lm1 <-lm(Sepal.Length ~ X, data = iris)iris_lm1 |>parameters() |>print_md()```### Let's see how that model looks:```{r}#| label: fig-iris-numeric-species-model#| fig-cap: "Model of `iris` data with numeric coding of `Species`"iris_plot1 <- iris |>ggplot(aes(x = X,y = Sepal.Length ) ) +geom_point(alpha = .1) +geom_abline(intercept =coef(iris_lm1)[1],slope =coef(iris_lm1)[2] ) +theme_bw(base_size =18)print(iris_plot1)```We have forced the model to use a straight line for the three estimated means. Maybe not a good idea?### Let's see what R does with categorical variables by default:```{r}#| label: tbl-iris-model-factor1#| tbl-cap: "Model of `iris` data with `Species` as a categorical variable"iris_lm2 <-lm(Sepal.Length ~ Species, data = iris)iris_lm2 |>parameters() |>print_md()```### Re-parametrize with no interceptIf you don't want the default and offset option, you can use "-1" like we've seen previously:```{r}#| label: tbl-iris-no-intcptiris_lm2_no_int <-lm(Sepal.Length ~ Species -1, data = iris)iris_lm2_no_int |>parameters() |>print_md()```### 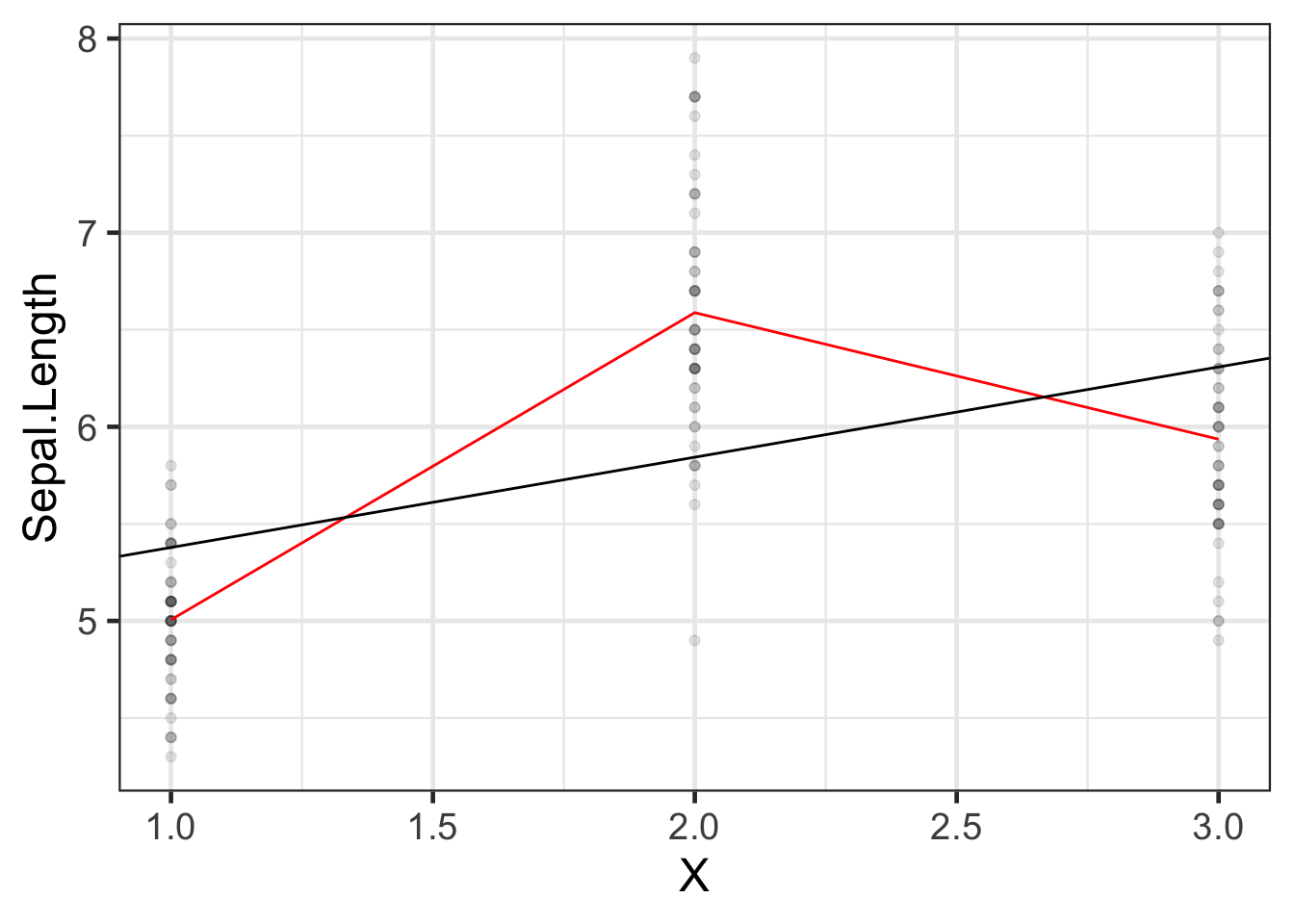Let's see what these new models look like:```{r}#| label: fig-iris-no-intcptiris_plot2 <- iris |>mutate(predlm2 =predict(iris_lm2) ) |>arrange(X) |>ggplot(aes(x = X, y = Sepal.Length)) +geom_point(alpha = .1) +geom_line(aes(y = predlm2), col ="red") +geom_abline(intercept =coef(iris_lm1)[1],slope =coef(iris_lm1)[2] ) +theme_bw(base_size =18)print(iris_plot2)```### Let's see how R did that:```{r}#| label: tbl-iris-model-matrix-factorformula(iris_lm2)model.matrix(iris_lm2) |>as_tibble() |>unique()```This format is called a "corner point parametrization" (e.g., in @dobson4e) or "treatment coding" (e.g., in @dunn2018generalized).The default contrasts are controlled by `options("contrasts")`:```{r}options("contrasts")```See `?options` for more details.---```{r}#| label: tbl-iris-group-point-parameterizationformula(iris_lm2_no_int)model.matrix(iris_lm2_no_int) |>as_tibble() |>unique()```This format is called a "group point parametrization" (e.g., in @dobson4e).There are more options; see @dobson4e §6.4.1 and the [`codingMatrices` package](https://CRAN.R-project.org/package=codingMatrices)[vignette](https://cran.r-project.org/web/packages/codingMatrices/vignettes/codingMatrices.pdf)(@venablescodingMatrices).## Ordinal covariates(c.f. @dobson4e §2.4.4)---::: notesWe can create ordinal variables in R using the `ordered()` function^[or equivalently, `factor(ordered = TRUE)`].::::::{#exm-ordinal-variable}```{r}#| eval: falseurl <-paste0("https://regression.ucsf.edu/sites/g/files/tkssra6706/","f/wysiwyg/home/data/hersdata.dta")library(haven)hers <-read_dta(url)``````{r}#| include: falselibrary(haven)hers <-read_stata(fs::path_package("rme", "extdata/hersdata.dta"))``````{r}#| tbl-cap: "HERS dataset"#| label: tbl-HERShers |>head()```:::---Check out `?codingMatrices::contr.diff`
